stożek geometrykz: Dany jest stożek o wysokości długości h i promieniu podstawy długości r, oblicz długość krawędzi sześcianu wpisanego w stożek w ten sposób, że dolna podstawa sześcianu zawiera się w podstawie stożka, a wierzchołki górnej podstawy sześcianu należą do powierzchni bocznej stożka. po narysowaniu: a− krawędź sześcianu h− wysokość stożka r − promień podstawy korzystając z podobieństwa:

h−a		h
	=
a		2r

ale nie pokrywa się odpowiedź z tą z książki − gdzie jest błąd?

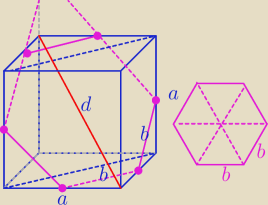
geometrykz: to może co innego: przekrojem sześcianu jest sześciokąt foremny, którego wierzchołkami są środki odpowiednich krawędzi sześcianu. Wiedząc, że pole tego sześciokąta jest równe 6√3, oblicz dł. przekątnej sześcianu. wprowadzam oznaczenia: a − krawędź sześcianu x − krawędź sześciokąta

	a		a
z tw. Pitagorasa: x2=(		)2+(		)2
	2		2

	a√2
x=
	2

Psz=6√3=6PΔ

	x2*√3
PΔ=		= 2√3x2
	4

6√3=6 * 2√3x² 1=2x²

	1
x2=
	2

	1
x=
	4

wracając do pierwszego równania(Pitagoras):

1		a√2
	=
4		2

	√2
a=
	4

	√6
d=a√3=
	4

odpowiedź to:2√6 i nie mogę się doszukać błędu.

geometrykz: hmm

geometrykz: nikt? naprawdę nie widzę błędów...

geometrykz:

Mila: To które masz źle?

geometrykz: i to i to, a w żadnym nie mogę doszukać się błędu

geometrykz: robiłem je po parę razy i za każdym razem takie same efekty.

Mila:

	a√2
b=
	2

P_{sześciokąta}=6*P_Δ 6*P_Δ=6√3 P_Δ=√3

	b2√3
PΔ=
	4

b2√3
	=√3
4

b²=4 b=2

	a√2
b=
	2

a√2
	=2
2

a√2=4

	4
a=		=2√2
	√2

d=a√3 d=2√2*√3 d=2√6 =====

geometrykz: dziękuję, odpowiedź się zgadza, za chwilę przeanalizuję tylko wyjdę z psem

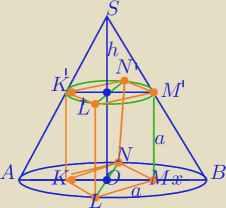
Mila: |OB|=r |BM|=x

	a√2
|OM|=
	2

	a√2
x=r−
	2

ΔSOB∼ΔMM'B⇔

h		a
	=		⇔
r		x

a*r=h*x

	a√2
a*r=h*(r−		)
	2

	a√2
a*r=h*r−h*		/ *2
	2

2a*r=2hr−h*a√2 2ar+h*a√2=2hr a(2r+√2*h)=2hr

	2h*r
a=
	2r+√2*h

geometrykz:

Mila: