Wartość bezwzględna
arek199602: Wyznacz wartości parametru m, dla których równanie |x−1|=m ma dwa pierwiastki różnych znaków.
I zał. x−1≥0
x≥1
zatem |x−1|=x−1
x−1=m
x=m+1
m+1≥1
m≥0
m∊<0; +
∞)
II zał. x−1<0
x<1
zatem |x−1|=−(x−1)=−x+1
−x+1=m
−x=m−1
x=−m+1
−m+1=<1
−m<0
m>0
uwzgl I i II
i m∊<0;+
∞)
W odpowiedziach jest wynik m∊(1; +
∞)
Mógłby ktoś powiedzieć gdzie popełniam bląd

pigor: ..., rozwiązanie masz np. takie
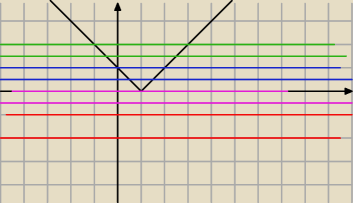
f(x)= |x−1}=m i f(0)=|0−1|=|−1|=1 ⇒ stąd i z wykresu
funkcji f proste
y=m i m∊R przecinają ten wykres
tak, że x
1x
2<0 ⇔
m>1 ⇒
m∊(1;+∞). ...