stereometria Rupii: W stożek o promieniu podstawy √3 i wysokości 2 wpisano graniastosłup prawidłowy trójkątny w taki sposób , że dolna podstawa graniastosłupa zawiera się w podstawie stożka , a wierzchołki górnej podstawy leżą na powierzchni bocznej stożka.Oblicz objętość graniastosłupa wiedząc że wszystkie jego krawędzie są równej długości. Proszę o pomoc.

Rupii:

Rupii: Pomoże ktos?

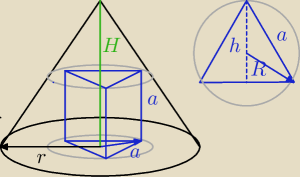
Raf131: Zrób sobie rysunek. a − krawędź graniastosłupa Następnie zobacz, że górna podstawa graniastosłupa (trójkąt równoboczny) będzie zawarta w okręgu, którego promień można uzależnić od wielkości a. Wyznacz promień tego okręgu w zależności od a, wiedząc, że w tym przypadku r₁ = ²₃h₁ h₁ − wysokość trójkąta równobocznego (górnej podstawy graniastosłupa) Następnie z podobieństwa trójkątów (dwa prostokątne, ten o długościach 2, √3, x oraz o długości r₁, 2−a, y, gdzie x, y przeciwprostokątne ) wyznacz długość a oraz objętość bryły.

dero2005:

dero2005:

Rupii: Powstaje mi że V=216/125 ,a w odpowiedziach jest że 54√3/125. Co robię żle mam proporcje 6−3a/a√3=2/√3

dero2005: H = 2 r = √3

	2		2		a√3		a√3
R =		hp =		*		=
	3		3		2		3

H		a		a
	=		=
r		r−R		3r−a√3   3

3Hr − Ha√3 = 3ar

	3Hr		6
a =		=
	3r+H√3		5

	a2√3*a		a3√3		54√3
V =		=		=
	4		4		125

Rupii: Dziękuję