Zadania trudne - geometria, trygonometria, ciągi - dla każdego coś dobrego:) Ludwik Montgomery: 1) Na bokach prostokąta o obwodzie 16cm opisano, jako na średnicach, półokręgi leżące na zewnątrz prostokąta. Zbadaj zapisując odpowiednią funkcję, dla jakich długości boków prostokąta, pole figury ograniczonej krzywą złożoną z tych czterech półokręgów jest najmniejsze. Oblicz pole. 2) Suma k początkowych wyrazów ciągu geometrycznego jest równa 3, a suma 2k początkowych wyrazów tego ciągu jest równa 18. Oblicz sumę 3k początkowych wyrazów tego ciągu. 3)Rozwiąż równanie (x−3)²*∥sin x∥= sin x w zbiorze {0,2π}. 4) Jeżeli przekątna trapezu równoramiennego zwiera się w dwusiecznej kąta ostrego i stosunek dłuższej podstawy do krótszej jest równy 2, to (prawda czy fałsz); a) Ramię jest równe krótszej podstawie b) przekątna jest prostopadła do jednego z ramion c) kąt ostry trapezu ma miarę 600. Proszę o naprowadzenie albo o częściowe zrobienie

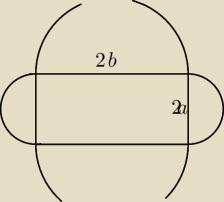
Qulka: obwód 16=4b+4a więc b=4−a Pole = πa²+πb²+4ab = πa²+π(4−a)²+4a(4−a)

Qulka: zad2

	1−qk
a1		= 3
	1−q

	1−q2k
a1		= 18
	1−q

1−q2k
	= 6
1−qk

i np delta

J: 3) dla sinx ≥ 0 ⇔ (x−3)²sinx = sinx ⇔ sinx[(x−3)² −1] = 0 ⇔ sinx = 0 lub [(x−3)² −1] = 0 ⇔ x = 0 lub x = π x = 4 lub x = 2 ( spełniają tylko x = 0 ,x = π , x = 2) dla sinx < 0 mamy: sinx[(x−3)² +1] = 0 ⇔ sinx = 0 ⇔ x = 2π

Ludwik Montgomery: Dziękuję, widzę, że można na was liczyć Qulka, mogłabyś mi jeszcze napisać, co dalej mam zrobić z 1 i 2, bo niestety jeszcze tego nie ogarniam...

Qulka: w 1 policzyć pochodną lub znaleźć współrzędne wierzchołka paraboli w 2 q^k=t i masz t²−6t+5=0

Ludwik Montgomery: Dziękuję

Ludwik Montgomery: Up

Ludwik Montgomery: Ktoś coś więcej?