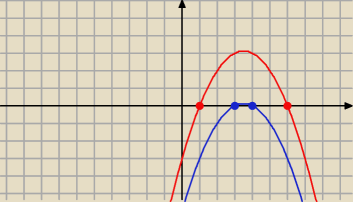
Zadanie z funkcji. Prosze o pomoc, pilne! Mateusz 13579: Parabola będąca wykresem funkcji kwadratowej f przecina oś x w punktach (1, 0) i (6, 0). Parabole tę przesunięto w dół o 3 jednostki i otrzymano wykres funkcji g, której miejscami zerowymi są liczby 3 i 4. Wyznacz wzory funkcji f i g w postaci ogólnej.

Janek191: x₁ = 1 x₂ = 6 więc

	x1 + x2
p =		= 3,5
	2

f(x) = a*( x − p)² + q = a*( x − 3,5)² + q g(x) = a*( x − 3,5)² + q − 3 g(3) = 0 ⇔ a*( −0,5)² + q − 3 = 0 ⇔ 0,25 a + q − 3 = 0 ⇒ q = 3 − 0,25 a zatem f(x) = a*( x − 3,5)² + 3 − 0,25 a f(6) = 0 ⇔ 6,25 a + 3 − 0,25 a = 0 ⇔ 6 a = − 3 ⇔ a = − 0,5 f(x) = −0,5*( x − 3,5)² + q f(1) = 0 ⇔ −0,5*6,25 + q = 0 ⇔ q = 3.125 f(x) = −0,5*( x − 3,5)² + 3,125 oraz g(x) = −0,5*( x − 3,50² + 0,125

Janek191: Dokończ Np. g(x) = −0,5*( x² − 7 x + 12,25) + 0,125 = − 0,5 x² + 3,5 x − 6,125 +0,125 g(x) = − 0,5 x² + 3 ,5 x − 6

Eta: f(x)=a(x−1)(x−6) (1,0) i (6,0) po przesunięciu tych punktów o 3 jednostki w dół otrzymamy punkty (1,−3) i (6,−3) należące do g(x) zatem g(x)= a(x−3)(x−4) i y=−3 i x=1 ⇒ −3=a*(1−3)(1−4) ⇒ a= −0,5 to : f(x)= −0,5(x−1)(x−6) i g(x)=−0,5(x−3)(x−4)