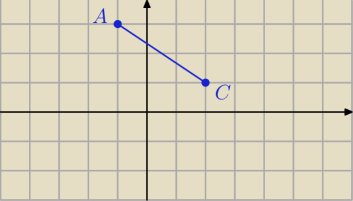
Geometria analityczna Rafal: http://iv.pl/images/95710462332714244904.jpg Hej, cześć, z jakich wzorów skorzystać w tym zadaniu? Tak wiem, można to od razu zobaczyć, ale ja chcę obliczyć. i jeszcze takie zadanko Punkty A(−1,3) i C(2,1) są przeciwległymi wierzchołkami kwadratu abc. Pole tego kwadratu jest wtedy równe?

yolex: długość AC to długość przekątnej. Pole=1/2d²

yolex: Środek tego okręgu to punkt przecięcia się symetralnych. Napisz równania dwóch symetralnych (pionową masz natychmiast) i rozwiąż układ równań.

Rafal: Jak wyznaczyć równanie symetralnej AC z zadania, co podałem obrazek?

Mila: 2) |AC|=√(2+1)²+(1−3)²=√9+4=√13

	1		13
P□=		**√132=
	2		2

========================

Mila: Do pierwszego napisz wsp. wierzchołków Δ, bo stronka nie otwiera sie u mnie.

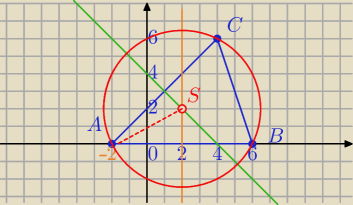
Rafal: Wyznacz współrzędne środka okręgu opisanego na trójkącie ABC A(−2,0) B(6,0) C(4,6)

Rafal: i gdzie znajdę wzór, którego użyłaś na pole kwadratu?

Mila:

	d2
Pole kwadratu liczysz jak pole rombu. P=
	2

Albo P=a² 2) Symetralna AB: x=2 3) Symetralna AC − zbiór punktów jednakowo odległych od końców odcinka A=(−2,0) C=(4,6) P(x,y) − dowolny punkt symetralnej √(x+2)²+(y−0)²=√(x−4)²+(y−6)² /² x²+4x+4+y²=x²−8x+16+y²−12y+36 4x+4=−8x+16−12y+36 12y=−12x+48 /:12 y=−x+4 S− środek okręgu obliczymy jako punkt przecięcia prostych x=2 i y=−x+4 x=2, y=2 S=(2,2) R=√(2+2)²+(2−0)²=√16+4=√20 Równanie okręgu (x−2)²+(y−2)²=20 Dobranoc

yolex: w szkole się to chyba pisze jako prostą prostopadłą do boku, przechodzącą przez środek. jak tak napisze to wszystkich zadziwi. i będzie się musiał tłumaczyć

Mila: Przecież nauczyciel zna ten sposób, a uczeń zdobywa wiadomości z różnych źródeł. Tylko jakoś uczeń nie jest ciekawy.