planimetria Rupii: Wśród wszystkich czworokątów wypukłych których suma długości przekątnych jest równa d ,wyznacz te ,które mają największe pole

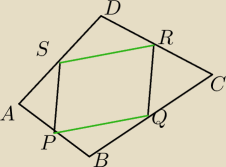
vaultboy: Niech [XYZ] oznacza pole figury XYZ Niech P,Q,R,S będą środkami boków odpowiednio AB,BC,CD,DA Z tw Talesa pokazujemy że PQRS jest równoległobokiem. Pokażemy, że [PQRS]=1/2[ABCD] Dowód: Niech [APS]=X, [BPQ]=Y, [CQR]=Z, [DRS]=T Wtedy z jednokładności [ABD]=4X [ABC]=4Y [CBD]=4Z [ADC]=4T, czyli 4X+4Z=[ABCD]=4Y+4T Zatem 2(X+Z)=2(Y+T)=1/2[ABCD] czyli 2(X+Y+Z+T)=[ABCD] Widać że PQRS=X+Y+Z+T c.k.d. Przyjmijmy AC=d/2 + 2c i BD=d/2 − 2c (sumują się do d) Wtedy z jednokładności PQ=d/4+c i PS=d/4−c Skoro pole ABCD ma być największe to pole PQRS ma być największe. [PQRS]=sin(<PQS)*PQ*PS=sin(<PQS)[(d/4)²−c²] pole tego będzie największe gdy c=0, bo najmniej odejmuję, a <PQS nie jest od tego zależny. Wtedy AC=BD oraz PQRS jest rombem. Największe pole mają te o równych przekątnych.

Rupii: Prosiłbym o rozwiązanie tego zadania za pomocą pochodnych Powinno powstać że są to czworokąty o równych przekątnych przecinających się pod kątem prostym.