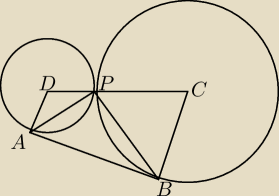
opis Marek: Witam. Czy zadanie jest wykonane poprawnie. Przepraszam za jakość. Dwa okręgi są styczne zewnętrznie w punkcie P. Poprowadzono prostą, styczną do obu okręgów odpowiednio w punktach A i B (A różne od B) Wykaż, że kąt ∡APB jest prosty. http://ifotos.pl/z/weraqwe/

yolex: jest ok

vaultboy: Niestety masz blefa. Chcesz pokazać że α+γ=90, ale ty tylko sprawdzasz, że wtedy <APB wynosi π/2

yolex: Nie zrozumiałeś idei, vaultboy. ABCD jest trapezem. Suma kątów przy ramieniu to 180. Ze związku między kątem dopisanym a środkowym ma α, 2α i γ ,2γ Po podzieleniu stronami (chyba w trzeciej linijce) ma α+γ=90,

yolex: czyli wykazał zależność, z której potem skorzystał.

vaultboy: Dowód: Niech <PAB=α i <PBA=β Wtedy z twierdzenia o stycznej i siecznej oraz z twierdzenia o kącie wpisanym i środkowym <ADP=2α i <PCB=2β. ADP i BCP są równoramienne zatem <CPB=90−β i <DPA=90−α. Stąd wniosek, że <APB=α+β Zatem <APB+<PBA+<BAP=α+β+β+α=180 czyli α+β=90 c.k.d.

vaultboy: Sry nie zauważyłem, że skorzystał z tego faktu że jest to trapez, nigdzie tego nie napisał. Zwracam honor

yolex: Zaznaczył kąty proste przy punktach styczności i skorzystał z sumy kątów w czworokącie. To w zasadzie to samo.

Marek: Napisałem że "Czworokąt ABCD ma 360 stopni"