Proszę o pomoc
nickum: Naszkicuj wykres funkcji f(x)=3x2+5x−2 i omów jej własności(zbiór
wartości,dziedzina,współrzędne wierzchołka,wartość minimalna lub maksymalna,przedziały
monotoniczności,oś symetrii)
29 mar 16:07
5-latek:
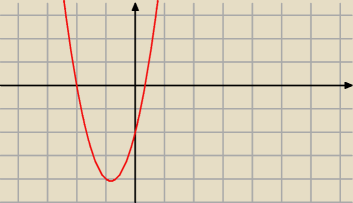
29 mar 16:13
nickum: Dzięki

29 mar 16:20
5-latek: Nie tak latwo
Dziedzina to ? −pisz
29 mar 16:22
5-latek: Na jakiej osi układu odczytujemy dziedzine funkcji ?
29 mar 16:24
nickum: dziedzina na y a zbiór wartości na x
29 mar 16:37
Janek191:
Coś nowego !

29 mar 16:38
kix: ot, dziwy natury

29 mar 16:39
nickum: no o obliczanie mi chodzi heh
29 mar 16:40
nickum: ja nie mogę tego pojąć,z matmą nie najlepiej u mnie jak zauważyłeś

29 mar 16:41
kix: jest akurat odwrotnie do tego co napisałeś o 16:37
29 mar 16:43
AS: A wiesz dlaczego masz kłopoty z matematyką,
bo nie chcesz.
29 mar 16:48
nickum: jak się od początku nie pojmie to potem tak to wychodzi
29 mar 16:52
Janek191:
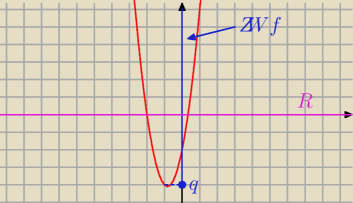
Dziedziną każdej funkcji kwadratowej jest zbiór liczb rzeczywistych ℛ
f : ℛ → ℛ i y = f(x) = 3 x
2 + 5 x − 2
a = 3 b = 5 c = − 2
| | − b | | − 5 | | 5 | |
p = |
| = |
| = − |
| |
| | 2a | | 2*3 | | 6 | |
Δ = b
2 − 4a*c = 5
2 − 4*3*(−2) = 25 + 24 = 49
Zbiór wartości
| | 49 | |
ZWf = < q ; + ∞ ) = < − |
| , + ∞ ) |
| | 12 | |
Kolor niebieski − ZWf
Kolor fioletowy − dziedzina funkcji f , czyli ℛ
29 mar 16:57
nickum: Dzięki

29 mar 17:07
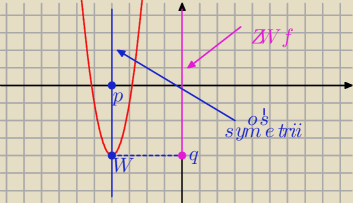
Janek191:
cd. Oś symetrii to x = p
czyli
========
Wierzchołek W = ( p , q )
czyli
====================
a = 3 > 0 , więc ramiona paraboli ( wykresu funkcji ) są skierowane ku górze, więc
funkcja przyjmuje najmniejszą wartość
==================
29 mar 17:19
Janek191:
cd.
Przedziały monotoniczności :
Dla x < p funkcja maleje , a dla x > p funkcja rośnie, czyli
| | 5 | | 5 | |
f maleje w ( − ∞ , − |
| ) , a f rośnie w ( − |
| , + ∞ ). |
| | 6 | | 6 | |
29 mar 17:22
Janek191:
29 mar 17:29





 Dziedziną każdej funkcji kwadratowej jest zbiór liczb rzeczywistych ℛ
f : ℛ → ℛ i y = f(x) = 3 x2 + 5 x − 2
a = 3 b = 5 c = − 2
Dziedziną każdej funkcji kwadratowej jest zbiór liczb rzeczywistych ℛ
f : ℛ → ℛ i y = f(x) = 3 x2 + 5 x − 2
a = 3 b = 5 c = − 2

