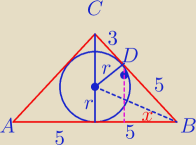
Planimetria Szymon69: W trójkąt równoramienny ABC, w którym |AC|=|BC| wpisano okrąg. Punkt D jest punktem styczności tego okręgu z ramieniem BC i dzieli to ramię na odcinki długości |BD|=5cm i |DC|=3cm. Oblicz |AD|.

Janek191:

3		x
	=
r		h

h² = 8² − 5² = 64 − 25 = 39 h = √39

h1		5
	=
h		8

	5		5
h1 =		*h =		*√39
	8		8

	25
x2 = 52 − (h1)2 = 25 −		*39
	64

	25
x =
	8

	55		25
I AD I2 = ( 10 − x)2 + (h1)2 = (		)2 +		*39
	8		64

	20√10
I AD I =		= 2,5√10
	8

Janek191:

3		x
	=		jest zbędne
r		h

Szymon69: dzieki