Pole wielokata zawartego w trójkącie scav1337: Punkty M i L leżą odpowiednio na bokach AB i AC trójkąta ABC, przy czym zachodzą równości |MB| = 3|AM| oraz |LC| = 5|AL|. Punkt S jest punktem przecięcia odcinków BL i CM. Pole trójkąta ABC jest równe 552. Oblicz pole czworokąta AMSL.

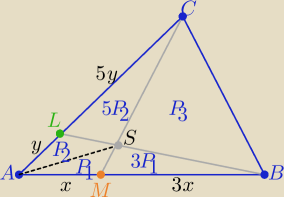
Eta: Mamy obliczyć pole : P(AMSL)=P₁+P₂ P(ABC)=552 W trójkątach AMC i BMC : 3*(6P₂+P₁)= 3P₁+P₃ ⇒ P₃=18P₂ W trójkątach: AML i BLC : 5*(4P₁+P₂)=5P₂+P₃ ⇒ P₃=20P₁

	10
to 18P2=20P1 ⇒ P2=		P1
	9

P(ABC)=4P₁+6P₂+P₃= 552 ( po podstawieniach otrzymujemy ⇒ 92P₁=1656 ⇒ P₁=18 to P₂=20 P(AMSL)= 38 j²