Geometria Blue: zad.1 Dwa boki trójkąta o polu S mają długość a i b. Znajdź promień okręgu stycznego do tych boków wiedząc, że jego środek należy do trzeciego boku. zad.2 W trójkącie ABC boki AC i BC są równe. Okrąg, którego średnicą jest wysokość CD trójkąta, przecina boki trójkąta w punktach dzielących te boki w stosunku m:n licząc od wierzchołka C. Wyznacz pole trójkąta, znając długość h wysokości CD.

prosta:

1		1
	ar+		br=S
2		2

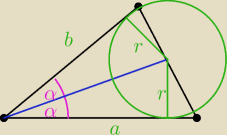
	2S
(a+b)r=2S −−−−> r=
	a+b

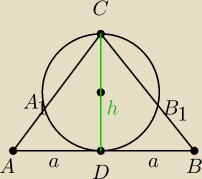
prosta: z tw. o odcinkach stycznych i siecznych: |AD|²=|AA₁||AC| a²=nx(n+m)x −−−−> a²=n(n+m)x² h²+a²=(m+n)²x² −−−−> (m+n)²x²=h²+n(n+m)x² x²(m²+2mn+n²−n²−mn)=h² −−−−> x²m(m+n)=h²

	h2		h2n(n+m)
x2=		więc a2=
	m(m+n)		m(m+n)

	n
a2=		h2
	m

	√ n		2ah		√ n
a=		h ...P=		=ah=		h2
	√ m		2		√ m

prosta: potwierdzi ktoś?

prosta:

Blue: Odpowiedzi się zgadzają. Wielkie dzięki I wybacz mi, że dopiero teraz odpisuję

Kacper: