Walka ze stereometrią Ruanda: Witam, bardzo zależy mi na tym zadaniu. W ostrosłupie prawidłowym trójkątnym kąt między ścianą boczną a podstawą jest równy α Oblicz cosinus kąta między ścianami bocznym tego ostrosłupa.

Janek191:

	√3
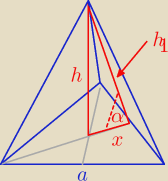
hp = a
	2

	1
x =		hp = a U{√3}{6
	3

więc

x
	= cos α
h1

√3   a   6
	= cos α
h1

	a √3
h1 =
	6 cos α

Janek191:

	3 a2
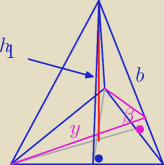
b2 = (0,5 a)2 + h12 = 0,25 a2 +
	36 cos2α

	1
b = √( 0,25 +		) a
	12 cos2α

y		h1
	=
a		b

	a h1
y =		= U{ a√3}{√9 + 3cos2α
	b

Janek191:

	a √3
y =
	√ 9 + 1cos2α

Janek191: Z tw. cosinusów a² = y² + y² − 2 y² cos β

	3a2		3 a2		6 a2
a2 =		+		−		*cosβ
	1   9 +   cos2α		1   9 +   cos2α		1   9 +   cos2α

	1
1 − cos β = 1,5 +
	6 cos2α

	1
cos β = − 0,5 −
	6 cos2α

====================== Pewnie się pomyliłem w rachunkach.

Janek191: Pewnie powinno być

	a√3
y =
	√9 cos2 α + 13

oraz

	1
cos β = − 0,5 cos2α −
	18

======================

prosta: z tw. cosinusów: a²=y²+y²−2y²cosβ

	a2
2y2cosβ=2y2−a2 −−−−> cosβ=1−
	2y2

i teraz:

	a 2		3a2		3a2(3cos2α+1)
b2=		+		−−−> b2=
	4		36cos2α		36cos2α

y		h1		a 2		b 2		3a2
	=		−−−−>		=		i h1=
a		b		y2		h12		36cos2α

mamy stąd:

	3a2(3cos2α+1)		36cos2α
cosβ=1−		*
	36cos2α		6a2

	3cos2α+1		1−3cos2α
cosβ=1−		=
	2		2

Ruanda: Dzięki bardzo sprawdziłam w odp jest ^1−3cos2α₂