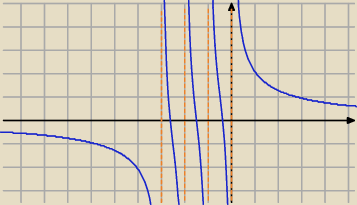
pracochłonne zadanie YushokU: Witam, Mam problem z zadaniem. Rozważmy funkcję:

	1		1		1		1
y=		+		+		+
	x		x+1		x+2		x+3

a)Oblicz pochodna funkcji b)Podaj przedziały monotoniczności c)Określ liczbę rozwiązań równania f(x)=0 d)Podaj liczbę rozwiązań równania f(x)=m w zależności od parametru m. Czy ono jest w jakiś sposób trikowe? Bo jestem strasznym leniuchem i nie chce mi się tego wymnażać wszystkiego. Tylko tyle mnie interesuje. Jeśli nie, to w takim razie dam sobie z nim radę

Qulka:

YushokU: Straszne to zadanie...

	4x3+18x2+22x+6
f(x)=
	x4+6x3+11x2+6x

Braun: Po co to zrobiłeś....

a		−a
	=
x		x2

	1		1		1
f'(x)=−		−		−
	x2		(x+1)2		(x+3)2

Qulka: wymnożył pewnie do miejsc zerowych

Mila: x≠0 i x≠−1 i x≠−2 i x≠−3 Miejsca zerowe:

	1		1		1		1
(		+		)+(		+		)=0⇔
	x		x+3		x+1		x+2

x+3+x		x+2+x+1
	+		=0
x*(x+3)		(x+1)*(x+2)

2x+3		2x+3
	+		=0⇔
x*(x+3)		(x+1)*(x+2)

	1		1
(2x+3)*[		+		]=0⇔
	x*(x+3)		(x+1)*(x+2)

	1		1
(2x+3)=0 lub [		+		]=0
	x*(x+3)		(x+1)*(x+2)

Teraz już nie jest straszne do dokończenia.

YushokU: Dobra, dzięki bardzo. Teraz da się to jakoś ładnie dokończyć,bo moim sposobem to bym siedział, siedział i dzielił i tak w kółko. Tak właśnie myślałem, że wyjdzie coś z tego całkiem fajnego

Mila: