nierowności wymierne z parametrem Jola: Witam czy ktoś mógłby mi to wytłumaczyć?

	(m+2)x2+x+m+2
Dla jakich wartości parametru m zbiorem rozwiazan nierownosci		<0
	x2−(m+5)x+9

jest zbior wszystkich liczb rzeczywistych?

yolex: z mianownika delta<0 (wtedy dziedziną jest R i mianownik jest zawsze dodatni)). Z licznika (a<0 i delta <0) lub (a=0 i b=0 i c<0) (wtedy licznik jest zawsze ujemny)

Dawid: Dziękuję bardzo, sprubuje sobie tak rozpisac, gdyby cos bylo nie tak to jeszcze sie tu odezwę

5-latek: Mam pytanie co do tego zadania Wiemy ze L(+) i M(−) to wyrazenie <0 a także L(−) M(+) to wyrażenie <0 mamy dla mianownika a>0 i delta <0 to mianownik będzie dodatni Teraz pytanie . A co będzie gdy przyjmę ze delta >0 przecież dla tych warunków mianownik tez przyjnuje wartości dodatnie i odpowiednich przedziałach

5-latek: I również w odpowiednim przedziale mianownik dla tych warunków czyli a>0 i Δ>0 mianownik jest ujemny

yolex: Jeśli rozwiązaniem ma być cały R, to dziedziną też musi być R, czyli mianownik nie może mieć miejsc zerowych.

5-latek: OK

	x2−(m+5)x+9
Natomiast jeśli nierownosc by była taka		<0 to wtedy Licznik
	(m+2)X2+x+m+2

zawsze dodatni a mianownik musi być ujemny

5-latek: Co do postu 21:48 A jeśli miejsca zerowe wyrzucę z rozwiązania ?

Qulka: aby mianownik zawsze ujemny to a<0 i Δ<0

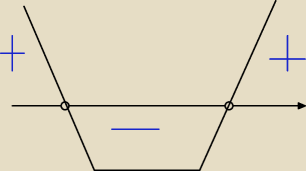
5-latek: Dziekuje Aniu tylko chodzilo mi bardziej o to ze jeśli mam tak jak tu na wykresie a>0 i delta >0 to ta funkcja w przedziale od x₁ do x₂ (bez x₁ i x₂ przyjmuje wartości ujemne a (−∞ x₁)U(x₂∞) wartości dodatnie . Ale rozumiem ze tak być nie może musi być cala albo nad osia oX albo pod osia

Qulka: tak bo jak wyrzucisz miejsca zerowe to nie będziesz szukał m j.w. tylko takiego by pasowało w miejsca zerowe jako wykluczenia w dziedzinie..więc to całkiem inna zabawa

5-latek: To rozumiem . jeszcze raz dziekuje