Kąty dowód Damian1996: Na przeciwprostokątnej AB trójkąta prostokątnego ABC zbudowano po przeciwnej stronie prostej AB niż punkt C, kwadrat ABDE. Udowodnij, że półprosta CS jest dwusieczną kąta ACB, gdzie punkt S jest punktem przecięcia się przekątnych kwadratu ABDE. Zauważyłem, ze AB jest średnicą okręgu opisanego na czworokącie ASCB, ale nie wiem jak to dalej pociągnąć A zapewne jestem już bliżej niż dalej końca

Damian1996: ?

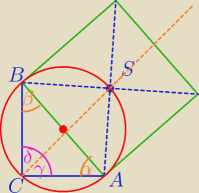
Mila: Dobrze zauważyłeś. Na czworokącie CASB można opisać okrąg, bo sumy kątów przeciwległych sa równe ( i mają po 180 ^o) ∡SCA i ∡SCB to kąty wpisane w okrąg oparte na takim samymłuku okręgu ( cięciwy AS i BS są równe )⇔ CS jest dwusieczną kąta prostego.

Damian1996: Wszystko jasne, dziękuję za pomoc

Mila:

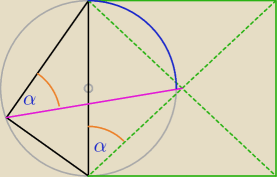
===: kąty wpisane oparte na tym samym łuku