Dowód P: Uzasadnij, że równanie ma w podanym przedziale co najmniej jeden pierwiastek. a) x³ + 3x −2= 0, <0,1> b)−x⁴+4x+3=0, <1,2>

Saizou : a znasz własnośc Darboux ?

P: Nie.

Saizou : a to zadanie ze studiów czy poziom LO ?

M: Z liceum 3 klasa rozszerzenie, ale nie było takich zadań i dziwię się, że mamy taką pracę domową

ICSP: Zadanie na własność Darobux.

yolex: Obie funkcje to wielomiany, więc są ciągłe. Oblicz ich wartości na końcach przedziałów. Powinny wyjść różnych znaków. Wtedy zgodnie z wyżej wymienioną własnością musi na tym przedziale istnieć argument, dla którego funkcja przyjmuje wartość zero.

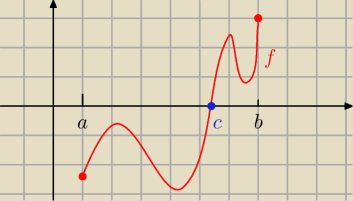
Saizou : Może napisze ogólniej, rozważmy funkcję f: [a,b]→R i jest ona ciągła (ps. większość funkcji jakie znasz to funkcje ciągłe, w szczególności wielomiany) zatem wartość funkcji w punkcie f(a)<0 ,a w punkcie f(b)>0, zatem iloczyn f(a)•f(b)<0 czyli istnieje punkt c∊(a,b), w którym wartość funkcji jest równa 0. stosując to np. dla a) mamy że f(0)=−2 f(1)=2 zatem f(0)•f(1)=−4<0 czyli istnieje punkt c∊(a,b) dla którego f(c)=0, a to jest równoważne z tym że istnieje miejsce zerowe w przedziale [a,b]

P: A. Ok. Dzięki. Rozumiem