Trygonometria - sprawdzenie Kuba: Witam. Chciałbym, aby ktoś sprawdzić, czy jest gdzieś błąd. Wiedząc, że alfa jest miarą kąta ostrego oraz ctg(alfa)=0,5 oblicz sinus, cosinus, i tg alfa. ctga=1/2 tga=2 tga=sina/cosa sina=2cosa podstawiam do trygonometrycznej jedynki sin2a + cos2a=1 1/3 + sin2a=1 3cos2a=1 sin2a=2/3 cosa= √1/3 sina= √2/3

Janek191:

	x		1
ctg α =		=		i 0o < α < 90o
	y		2

więc x = 1 i y = 2 , więc r² = x² + y² = 1 + 4 = 5 ⇒ r = √5 i dlatego

	y		2		2 √5
sin α =		=		=
	r		√5		5

	x		1		√5
cos α =		=		=
	r		√5		5

	y
tg α =		= 2
	x

Kuba: Nie rozumiem dlaczego sinusa i cosinusa mam źle.

Janek191: Boś źle wyliczył

Kuba: Nie mogę tego wyliczyć z trygonometrycznej jedynki?

Janek191: Widocznie nie możesz, jeżeli nie wyliczyłeś.

Janek191: tg α = 2

sinα
	= 2
cos α

sin α = 2 cos α i sin²α + cos²α = 1 więc ( 2 cos α)² + cos²α = 1 4 cos² α + cos²α = 1 5 cos²α = 1

	1
cos2α =
	5

	1		1		√5
cos α = √		=		=
	5		√5		5

Kuba: Nie dałem do nawiasu! ok dzięki, teraz wiem, co mam źle

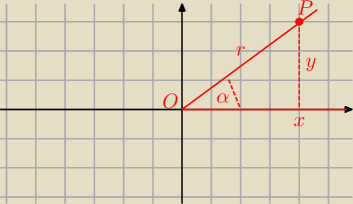
Janek191: Lepszy jest " mój " sposób P = ( x, y) r = I OP I r² = x² + y²

	y
sin α =
	r

	x
cos α =
	r

	y
tg α =
	x

	x
ctg α =
	y

5-latek: Albo tez wiedzac ze tgx=2 to sin²x= 1+tg²x = sin²x=5 to |sinx|= √5 cosx= √1−sin²x

Kuba: Żeby nie zakładać tematu 2 mam 2 zadanie: Uzasadnij, że: cosa + cosa * tg²a = 1/cosa cosa + cosa * sin²a/cos²a = 1/cosa cosa + sin²a/cosa = 1/cosa i co mam dalej z tym zrobić?

yolex: Janek191: Twój sposób może być lepszy pod warunkiem, że będzie poprawny, a nie tylko będzie dawał poprawny wynik. Nie możesz napisać: "więc x=1, y=2", bo to nie jest prawdziwy wniosek. Albo pisz "bez straty ogólności rozważań mogę przyjąć, że x=1, y=2", albo "x=a, y=2a" i dalej wyliczasz z a, które się później redukuje. Nie ma sposobów lepszych i gorszych obiektywnie. Są lepsze dla kogoś i gorsze dla kogoś.

yolex: Sprowadź do wspólnego mianownika i w liczniku masz jedynkę.

Janek191:

	sin2α		sin2α
cos α + cos α* tg2α = cos α+ cos α*		= cos α +		=
	cos2α		cos α

	cos2α		sin2α		cos2α + sin2α		1
=		+		=		=
	cos α		cos α		cos α		cos α

Kuba: Yolex super, dzięki

Kuba: Kolejne zadanko: Oblicz pole i obwód trójkąta o bokach długości 3 i 4 cm i kącie o mierze 120cm między tymi bokami. Wiem, że wysokość podzieli go na 2 trójkąty o wymiarach 90 stopni 30 stopni i 60 stopni, ale nie wiem co z tym zrobić dalej, gdyż wtedy tak jakby ta sama długosc boku w obu trójkątach miałaby różną długość

prosta: hmmm....wysokość niekoniecznie podzieli kąt w ten sposób.... w tym zadaniu zadziała wzór na pole trójkąta z sinusem: P=0,5bcsinα

yolex: wzór cosinusów da ci długość trzeciego boku. Jesli jesteś na podstawie, to pewnie da się to inaczej, bo w podstawie nie ma tego wzoru. za to w tablicach jest.

prosta:

	√3
P=6sin120o i sin120o=sin60o=
	2