dowód, planimetria tris: Wykaż, że jeżeli a,b, c są długościami boków trójkąta a kąt α jest kątem wewnętrznym zawartym

	a2
między bokami b i c to		+ cosα ≥1
	2bc

próbowałam z tw cosinusów, ale jak na razie z marnym skutkiem

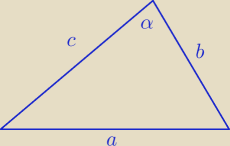
Janek191: a² = b² + c² − 2b*c cos α / : 2 b*c

a2		b		c
	=		+		− cos α
2 b*c		2c		2b

a2		b		c
	+ cos α =		+
2 b*c		2c		2b

a2		b2 + c2
	+ cos α =		≥ 1
2 b*c		2 b*c

bo

	b2 + c2
( b − c)2 ≥ 0 ⇔ b2 − 2 b*c + c2 ≥ 0 ⇔ b2 + c2 ≥ 2b*c ⇔		≥ 1
	2b*c

Janek191: Dlatego, że a > 0 , b > 0 , c > 0

tris: dziękuje bardzo! nie wpadłabym na te końcowe przekształcenia

Janek191: Trening czyni mistrza