Planimetria xyz: W trójkącie prostokątnym dwusieczna kąta prostego dzieli przeciwprostokątną w stosunku 2:3. W jakim stosunku dzieli przeciwprostokątną wysokość poprowadzona z wierzchołka kąta prostego?

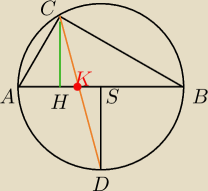
vaultboy: Niech pomarańczowy odcinek będzie dwusieczną, S będzie środkiem okręgu opisanego na ABC, D punktem przecięcia dwusiecznej z okręgiem opisanym, K punktem przecięcia dwusiecznej z bokiem AB, H spodkiem wysokości z C. Lemat: DS jest prostopadłe do AB. Dowód: AS=SB więc wystarczy pokazać, że AD=DB (wysokość trójkąt równoramiennego jest prostopadła do pewnego boku), ale <ACD=<BCD , bo CD jest dwusieczną. Zatem łuki AD i BD są równej długości z twierdzenia o kącie wpisanym w okrąg. Czyli odcinki AD i BD są sobie równe. c.k.d. Z założeń AK=2a i KB =3a dla pewnego a Widać, że <CKH=<DKS i <CHK=<DSK=π/2 zatem △CKH jest podobny do △DKS AB=5a ⇒ 5a/2=AB/2=AS czyli KS=AS−AK=a/2. SD=5a/2 bo jest to promień okręgu. Z podobieństwa trójkątów wyżej wymienionych otrzymuję 5=(5a/2)/(a/2)=SD/SK=CH/HK czyli CH=5HK Oznaczmy HK=x Oczywiście CS=5a/2 Z Pitagorasa dla trójkąta CHS mam CH²+HS²=CS² czyli (5x)²+(x+a/2)²=(5a/2)² Mamy równanie kwadratowe z parametrem a i wyliczamy stąd x. Wychodzi jedynie x=24a/52 Zatem AH=AK−KH=2a−24a/52=80a/52 HB=AB−AH=5a−80a/52=180a/52 Nasz stosunek AH/HB=80/180=4/9