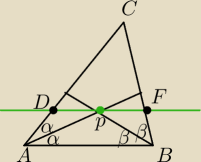
dowód w trójkącie reyg: W trójkącie ABC poprowadzono dwusieczne kątów A i B a następnie przez punkt ich przecięcia prostą l, równoległą do boku AB. Prosta l przecina bok AC w punkcie D, a bok BC w punkcie F. Wykaż, że |DF|=|AD|+|BF| Jakieś wskazówki ? nie mam pomysłu jak to w ogóle ugryźć.

Tadeusz: zauważ, że ∡APD=α zatem trójkąt ABD jest równoramienny itd

Tadeusz: oczywiście trójkąt APD a nie ABD

reyg: widzę to! dziękuję