monotoniczność ciągu
ert: proszę o sprawdzenie czy nie popełniłam gafy

an= −2n
2+1
an+1= −2(n+1)
2+1 zastosowałam wzór skróconego mnożenia i
−2n
2+2n+1
an+1−an= (−2n
2+2n+1)−(−2n
2+1)
−2n
2+2n+1−2n
2−1=
2n+2 lub 2n−2
problem z + i − zostanie u mnie na wieki zawsze coś pokręcę proszę o sprawdzenie

27 mar 23:58
Qulka: następny to −2n2−4n−2
28 mar 00:00
Qulka: jeszcze +1
28 mar 00:00
yolex: an+1=−2n2−2n−1 i dalej według tego różnica wynosi −2n−2
28 mar 00:02
yolex: przepraszam, nie zauważyłam pomyłki −2n2−4n−2 i odpowiednio −4n−2
28 mar 00:03
ert: czyli mam liczyć dalej ? −2n2−4n−2+1 ?
a wynik który poprawny

2n+2 lub 2n−2
dla mnie chyba już za póżno nie myślę już
28 mar 00:05
yolex: Myślę co innego, piszę co innego.

a
n+1= −2n
2−4n−1. Dalej bez zmian.
28 mar 00:06
Qulka: r= (−2n2−4n−1)−(−2n2+1)= −4n−2 =−2(2n+1)
nawias dodatni z przodu minus więc <0 więc malejacy
28 mar 00:07
yolex: wynik −4n−2
28 mar 00:08
Qulka: kwadraty Ci się skracają, bo zmieniasz znak
28 mar 00:08
Piotr:
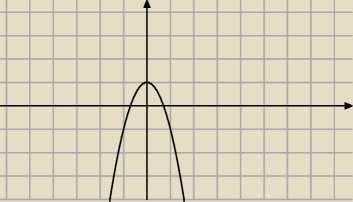
28 mar 00:11
ert: tak wiem że 2n
2 mi się poskracają i wtedy zostaje mi 2n−2

i lecimy dalej zgubiłam się tu
−2n
2+2n+1− − 2n
2−1=


?
28 mar 00:24
Qulka: −2n2−4n−1)−(−2n2+1)= −4n−2 = −2(2n+1)
nawias dodatni z przodu minus więc <0 więc malejacy
28 mar 00:27
ert: Dziękuję wam za pomoc uciekam spać ale jutro zasiądę do tego zadanka i jeszcze raz z pomocą
waszych wskazówek poprawię błędy

dobranoc i bardzo dziękuję

28 mar 00:40
ert: an= −2n
2+1
an+1= −2(n+1)
2+1
−2n
2+2n+1
an+1−an= (−2n
2+2n+1)−(−2n
2+1)
−2n
2+2n+1−2n
2−1=
−2n
2−4n−2+1
r= (−2n
2−4n−1)−(−2n
2+1)= −4n−2 =−2(2n+1)
Czy tak ma wyglądać poprawnie przepisane zadanie czy znowu coś namieszałam jeżeli namieszałam
proszę
napiszcie mi od początku do końca to zadanie bo zwariuje

29 mar 19:34
Qulka: ech...

od początku do końca to tak:
a
n = −2n
2+1
a
n+1 = −2(n+1)
2+1= −2(n
2+2n+1)+1= −2n
2−4n−1
a
n+1 − a
n = (−2n
2−4n−1)−(−2n
2+1)= −4n−2 =−2(2n+1) <0 malejący
30 mar 10:37
ert: Qulka: Jesteś wielka

Dziękuję

31 mar 21:12
 an= −2n2+1
an+1= −2(n+1)2+1 zastosowałam wzór skróconego mnożenia i
−2n2+2n+1
an+1−an= (−2n2+2n+1)−(−2n2+1)
−2n2+2n+1−2n2−1=
2n+2 lub 2n−2
problem z + i − zostanie u mnie na wieki zawsze coś pokręcę proszę o sprawdzenie
an= −2n2+1
an+1= −2(n+1)2+1 zastosowałam wzór skróconego mnożenia i
−2n2+2n+1
an+1−an= (−2n2+2n+1)−(−2n2+1)
−2n2+2n+1−2n2−1=
2n+2 lub 2n−2
problem z + i − zostanie u mnie na wieki zawsze coś pokręcę proszę o sprawdzenie 
 2n+2 lub 2n−2
dla mnie chyba już za póżno nie myślę już
2n+2 lub 2n−2
dla mnie chyba już za póżno nie myślę już
 an+1= −2n2−4n−1. Dalej bez zmian.
an+1= −2n2−4n−1. Dalej bez zmian.

 i lecimy dalej zgubiłam się tu
−2n2+2n+1− − 2n2−1=
i lecimy dalej zgubiłam się tu
−2n2+2n+1− − 2n2−1= 
 ?
?
 dobranoc i bardzo dziękuję
dobranoc i bardzo dziękuję 

 od początku do końca to tak:
an = −2n2+1
an+1 = −2(n+1)2+1= −2(n2+2n+1)+1= −2n2−4n−1
an+1 − an = (−2n2−4n−1)−(−2n2+1)= −4n−2 =−2(2n+1) <0 malejący
od początku do końca to tak:
an = −2n2+1
an+1 = −2(n+1)2+1= −2(n2+2n+1)+1= −2n2−4n−1
an+1 − an = (−2n2−4n−1)−(−2n2+1)= −4n−2 =−2(2n+1) <0 malejący
 Dziękuję
Dziękuję 