. afc:

	|x|−3
f(x) =
	|x|−2

Dla jakich wartości b prosta y=x+b ma z wykresem funkcji f dwa punkty wspólne?

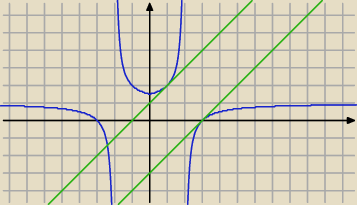
Qulka: dla b=1 lub b=−3

afc: da się to jakoś policzyć? bo jak przyrównuję wzór funkcji do równania prostej, a potem Δ>0 to wychodzi przedział

Qulka: weź tylko dodatnią część i Δ=0 albo z pochodnych albo graficznie

52: Witajcie Właśnie rozwiązałem sobie to zadanie i zastanawiam się czemu tylko dla dodatnich muszę?

afc: a ja nie wiem, dlaczego Δ=0 skoro mają być dwa punkty wspólne...

Qulka: nie musisz

Qulka: bo ten jeden punkt jest styczny czyli pierwiastek podwójny czyli Δ=0 patrząc na obrazek podejrzewam że tam masz raczej równanie 3 stopnia, wiec tego się deltą nie liczy ale jak Ci się udaje ja zrobiłam graficznie

52: wychodzi równanie kwadratowe...

Godzio: Bo każda prosta postaci y = x + b będzie miała punkt wspólny z wykresem funkcji dla x < 0. Dlaczego? Niech x < 0 (x + b)(x + 2) = x + 3 x² + x(b + 2) + 2b = x + 3 x² + x(b + 1) + 2b − 3 = 0 Δ = (b + 1)² − 4(2b − 3) = b² + 2b + 1 − 8b + 12 = b² − 6b + 13 Δ_b = 36 − 52 < 0, zatem Δ > 0 dla każdego rzeczywistego b. x₁ + x₂ = − b − 1 < 0 ⇒ b > −1

	3
x1x2 = 2b − 3 > 0 ⇒ b >
	2

	3
Czyli dla b >		mamy dwa pierwiastki ujemne, z rysunku widać, że jeżeli będą dwa ujemne,
	2

to i trzeci się pojawi (formalnie można to pokazać sprawdzając istnienie pierwiastków dla x >

	3
0 i b >		− wyjdzie, że istnieje, a co za tym idzie nie są spełnione warunki zadania).
	2

Pozostaje zatem pokazać, że dla x > 0 istnieje dokładnie jeden pierwiastek (czyli Δ = 0) i mamy to co chcieliśmy

52:

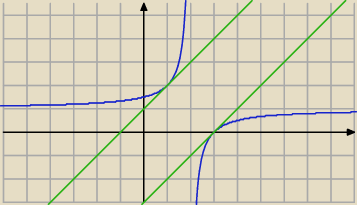
Qulka: bierzesz tylko dodatnie bo masz moduł i liczysz tylko Δ=0 bo tak naprawdę masz 1 punkt wspólny..drugi wynika z symetrii funkcji i jak podzielisz na dwie części się nie pojawia

Qulka: