Przekrój ostrosłupa
mat: Wszystkie krawędzie prawidłowego ostrosłupa czworokątnego mają długość a. Oblicz pole
przekroju płaszczyzną poprowadzoną przez środku dwóch sąsiednich krawędzi podstawy i środek
wysokości ostrosłupa.
Mam policzone pole prostokąta i nie wiem jak trzeba obliczyć pole tego trójkąta składającego
się na przekrój (nie wiem do którego trójkąta jest on podobny).
Pole prostokąta mam: a2√24.
pomoże ktoś?
27 mar 19:29
mat:
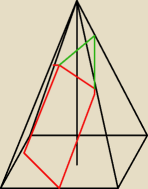
27 mar 19:45
mat: chodzi mi o ten zielony trójkącik

27 mar 19:46
Kret:
czy na pewno czerwony czworokąt jest prostokątem?
27 mar 19:50
mat: tak

pani nam mówiła
27 mar 19:52
Kret:
to napisz tak w rozwiązaniu − "wg pani czworokąt jest prostokątem", jakoś trzeba ten
fakt uzasadnić
27 mar 20:15
mat: ooo matko ja wiem dlaczego, wysokość tego ostrosłupa jest równa przekątnej kwadratu, jeżeli
płaszczyzna przechodzi przez połowę tej wysokości to to musi być prostokąt bo przechodzi też
przez środki krawędzi

27 mar 20:26
mat: Czy ktoś potrafi mi pomóc odnośnie tego trójkąta?

27 mar 20:27
mat: 
27 mar 20:46
Qulka:
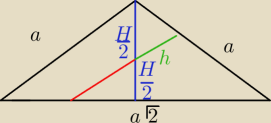
27 mar 20:55
Qulka: zielone h=a/4
27 mar 21:03
Qulka: pole zielonego trójkąta to
27 mar 21:04
Mila:
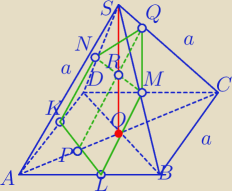
Odcinek PR łączy środki boków ΔAOS , zatem jest równoległy do AS i równy jego połowie.
Podobnie:
Odcinek PQ jest równoległy do AS , zatem
ΔPQC ∼ΔSAC⇒
| | 1 | | a√2 | | 1 | | a2√2 | |
PΔMNQ= |
| * |
| * |
| a= |
| |
| | 2 | | 2 | | 4 | | 16 | |
Dokończ
27 mar 21:06


 pani nam mówiła
pani nam mówiła




 Odcinek PR łączy środki boków ΔAOS , zatem jest równoległy do AS i równy jego połowie.
Odcinek PR łączy środki boków ΔAOS , zatem jest równoległy do AS i równy jego połowie.