Dowodzenie dotyczące promienia okręgu wpisanego w trójkąt FCB17: Od trójkąta ABC odcięto, prostymi równoległymi do boków trójkąta i stycznymi do koła wpisanego w ten trójkąt, trzy trójkąty narożne. Udowodnij, że suma długości promieni kół wpisanych w odcięte trójkąty jest równa długości promienia koła wpisanego w trójkąt ABC.

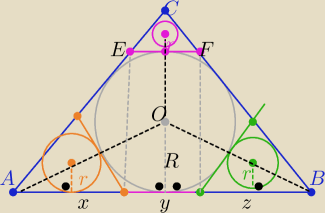
Eta: Trójkąty odcięte w narożach są podobne do trójkąta ABC z cechy (kkk) x+y+z= |AB| i |EF|=y

rA		R		xR
	=		⇒ rA=
x		|AB|		|AB|

rB		R		zR
	=		⇒ rB=
z		|AB|		|AB|

rC		R		yR
	=		⇒ rC=
y		|AB|		|AB|

+ −−−−−−−−−−−−−−−−−−−−

	x+y+z		|AB|
rA+rB+rC=		*R =		*R = R
	|AB|		|AB|

c.n.u