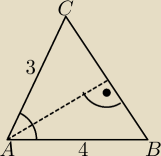
Oblicz Damian: Boki trójkąta ABC mają dlugosci: |AB|=4 |BC|=√3 |AC|=3 a)Oblicz cos(∡bac) b)Oblicz pole P trojkąta ABC c) Oblicz dlugość odcinka łączącego wierzcholek C z środkiem boku AB a) √3=3²+4²−2*3*4*cosα 3=9+16−24cosα 24cosα=22

	11
cosα=
	12

	1
b) P=		*ah
	2

	1		√3
P=		*4*
	2		2

P=√3 c) A wierzcholek mozna policzyc z tw.pitagorasa?

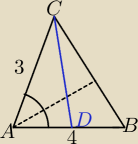Damian: Niestety w podpunkcie c) niemozna policzyc tego z tw pitagorasa bo nie powstanie trojkat prostokatny. Z twierdzenia cosinusow mozna?

	11
cosα=
	12

	11
|CD|2=32+42−2*3*4*cos
	12

pigor: ... , z ΔADC i tw. cosinusów: CD²=3²+2²−2*3*2*cos(BAC)=13−12*¹¹₁₂=13−11=2 ⇒|CD|=√2 .