ciągi
3rdpitch: 1. Trzy liczby, których suma = 126 tworzą ciąg geometryczny. Jeśli pierwszą zwiększymy o 13, a
trzecią o 67 to o trzymamy ciąg arytmetyczny. Wyznacz te liczby.
robiłem to tak:
a+b+c=126
b
2=ac
2b=a+c+80
a+c=2b−80
| | 206 | |
2b−80+b=126 ==> 3b=206 => b= |
| |
| | 3 | |
nie wychodzi mi nic z tego dalej, coś zrobiłem źle?
2. Wyznacz równanie stycznej do paraboli y=−2x
2+15x−22 nachylonej do osi OX pod kątem 135*
27 mar 15:05
J:
1) (x,y,z)
x + y + z = 126
y2 = x*z
2y = (x+13) + (z +67)
27 mar 15:18
Tadeusz:
1) b wyliczyłeś dobrze ... można oczywiście prościej je wyznaczyć ... ale wynik OK
dalej: b/q+b+bq=126
206/3(1/q+1+q)=126
27 mar 15:20
3rdpitch: a w drugim? wiem, że tg135 czyli ileśtam to jest współczynnik a w równaniu prostej... policzę
pochodną (y)' ale przecież do równania potrzebuję mieć x0 żeby policzyć f(x0) i
f'(x0)
27 mar 15:28
J:
przyrównaj pochodną do tg1350
27 mar 15:31
J:
−4x + 15 = − 1 ⇔ x = 4 ( x0 = 4)
27 mar 15:36
3rdpitch: dzięki

27 mar 15:38
J:
styczna: y = −(x − 4) + 6 ⇔ y = − x + 10
27 mar 15:38
J:
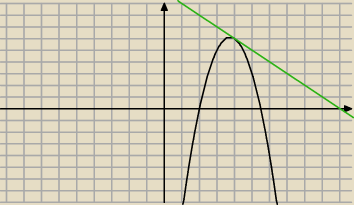
27 mar 15:39
3rdpitch: 3. Wyznacz wszystkie wartości parametru p dla których wielomian ma pierwiastek podwójny.
W(x)=x
3+px−16
4. Wyznacz wszystkie wartości parametru m dla których mniejszy pierwiastek równania
(m−2)x
2+(2m+1)x+1=0 jest mniejszy od 1, ale większy od 2
nie rozumiem w ogóle jak może być mniejszy od 1 a większy od 2? tu jest chyba błąd w zadaniu.
Nawet jeśli tak jest to mam mały problem z wyliczeniem dla jakich m mniejszy pierwiastek jest
mniejszy od 1.
Δ=4m
2+9
x1= U{{−2m−1−
√4m2+9}{2m−4}<1
| | −4m+3−√4m2+9 | |
dochodzę do takiej nierówności: |
| <0 |
| | 2m−4 | |
pierwszy czynnik <0 lub drugi <0
mam właśnie problem z pierwszym, jest tutaj pierwiastek i nie wiem co z nim zrobić.
robiłem to tak:
√4m2+9 > −4m+3 i zał: −4m+3≥0
27 mar 15:46
3rdpitch: to ostatnie próbowałem podniesc do kwadratu, ale czy mogę?
27 mar 15:47
J:
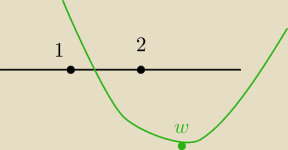
to jest ta sytuacja .. zauważ: x
w > 2 oraz f(1) > 0 oraz f(2) < 0
rozpatrujesz dwa przypadki: m − 2 > 0 oraz m− 2 < 0
27 mar 15:50
Tadeusz:
uruchom wyobraźnię −

27 mar 15:51
J:
tak ... jest bład: mniejszy od 2 , a większy od 1
27 mar 15:51
J:
no nie może coś być jednocześnie mniejsze od 1 i wieksze od 2

27 mar 15:52
Tadeusz:
drugi przypadek czyli a<0 czyli parabola smutna też rozważyć musisz −

27 mar 15:53
J:
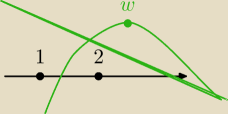
teraz : x
w > 2 , ale f(1) < 0 i f(2) > 0
27 mar 15:56
3rdpitch: ten warunek xw>0 jest konieczny? istnieje chyba parabola której mniejszy pierwiastek jest
pomiędzy 1 a 2, a x wierzchołka jest mniejsze od 2
27 mar 17:18
3rdpitch: pierwsza opcja:
I. m−2>0 ==> m>2
II. f(1)>0 ==> m>0
| | 5 | |
III. f(2)<0 ==> m< |
| wychodzi z tego zbiór pusty Φ |
| | 8 | |
druga opcja:
I: m−2<0 ==> m<2
II. f(1)<0 ==> m<0
| | 5 | |
III. f(2)>0 ==> m> |
| z tego również wychodzi zbiór pusty |
| | 8 | |
27 mar 17:27


 to jest ta sytuacja .. zauważ: xw > 2 oraz f(1) > 0 oraz f(2) < 0
rozpatrujesz dwa przypadki: m − 2 > 0 oraz m− 2 < 0
to jest ta sytuacja .. zauważ: xw > 2 oraz f(1) > 0 oraz f(2) < 0
rozpatrujesz dwa przypadki: m − 2 > 0 oraz m− 2 < 0



 teraz : xw > 2 , ale f(1) < 0 i f(2) > 0
teraz : xw > 2 , ale f(1) < 0 i f(2) > 0