Oblicz pole wycinka koła
Damian:
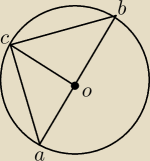
|cb|=3
|ca|=
√3
Z rysunku mozna stwierdzic ze kąt aob jest polpelny czyli 180stopni
Kąt acb ma wowczas 90stopni.
27 mar 14:07
J:
tak .. ∡acb = 900
27 mar 14:09
Damian: Ale czy odcinek |co| dzieli wtedy ten kąt na polowe?
27 mar 14:10
J:
nie , bo trójkąt nie jest równoramienny ( rysunek przkłamuje rzeczywisyość)
27 mar 14:12
Marek216: Którego wycinka ?
27 mar 14:13
Damian:
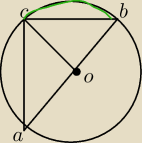
Aaa przepraszam nie zaznaczylem...
27 mar 14:18
Marek216: r to połowa średnicy którą obliczysz z twierdzenia pitagorasa. Mając długości promieni i boku
cb z funkcji trygonometrycznych możesz obliczyć kąt( ewentualnie z twierdzenia cosinusów)
27 mar 14:22
Damian: Wiec jesli ∡acb=90stopni to ∡bac=30 a ∡cba=60?
Z tego mozna ustalic ze |cb| to a
√3=3 wiec a=
√3 czyli odcinek |ca|. Zatem srednica jest
rowna2
√3 
27 mar 14:23
J:
Δ cob − równoramienny (r,r,3)
policz r , potem z tw.cos kąt: cob
27 mar 14:23
J:
tak .. i r = 3 ..zatem Δ cob jest równoboczny ... zatem ?
27 mar 14:25
Marek216: Czekaj nie rozpędzaj się z trojkąta prostokątnego wyznaczasz przeciwprostokątną jeżeli wyjdzie
ci 2√3 to kąty mówisz dobre ale nie odwrotnie kąty możesz ustalić na podstawie długości
boków ale nie odwrotnie w tym przypadku
27 mar 14:26
J:
d = 2√3 ⇒ r = 3 ... i masz trójkąt równoboczny ( Δ cob )
27 mar 14:27
J:
ajj... r = √3 ... sorry
27 mar 14:28
Marek216: Jeżeli d = 2
√3 to promień nie może być równy 3 panie J. Promień to połowa średnicy.

27 mar 14:30
J:
zatem: Δ aoc jest równoboczny
27 mar 14:31
J:
poprawiłem ...

27 mar 14:31
Damian: Dzieki wszystkim

Juz od momentu upewnienia sie ze srednica ma tyle ile podalem reszta poszla
gladko

27 mar 14:40
 |cb|=3
|ca|=√3
Z rysunku mozna stwierdzic ze kąt aob jest polpelny czyli 180stopni
Kąt acb ma wowczas 90stopni.
|cb|=3
|ca|=√3
Z rysunku mozna stwierdzic ze kąt aob jest polpelny czyli 180stopni
Kąt acb ma wowczas 90stopni.
 Aaa przepraszam nie zaznaczylem...
Aaa przepraszam nie zaznaczylem...



 Juz od momentu upewnienia sie ze srednica ma tyle ile podalem reszta poszla
gladko
Juz od momentu upewnienia sie ze srednica ma tyle ile podalem reszta poszla
gladko 