przekątne w wielokątach Mira: Ośmiokąt wypukly przecięto prostą na dwa wielokąty, z ktorych jeden ma 5 przekątnych, a drugi ponad dwa razy więcej. Ile przekątnych może mieć drugi wielokąt?

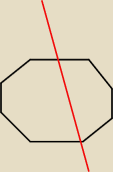
Basia: Wydaje mi się, że to niemożliwe.

	n(n−3)
liczba przekątnych n−kąta =
	2

czyli

n(n−3)
	=5
2

n(n−3)=10 n²−3n−10=0 Δ=9+40=49 √Δ=7

	3−7
n1=		=−2 odpada
	2

	3+7
n2 =		= 5
	2

czyli pierwszy musi być pięciokątem ⇒ drugi musi być sześciokątem i ma

6*3
	=9 przekątnych
2

chyba, że istnieje jakaś inna możliwość odcięcia tą prostą pięciokąta, której ja nie widzę

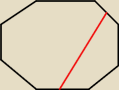
Miś: Tak należy podzielić, wtedy mamy pięciokąt i siedmiokąt.

Basia: Widziałam Misiu. Też sobie tak na kartce najpierw nabazgrałam, ale nabazgrałam i nie doliczyłam się siódmego wierzchołka. A potem już się zasugerowałam i klapa. Oczywiście tak musi być.