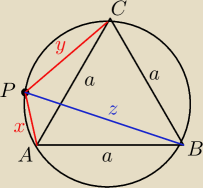
okręgi i trójkąty YushokU: Witam, Zadanko z planimetrii. Dany jest trójkąt równoboczny ABC wpisany w okrąg. Punkt P leży na krótszym łuku AC. Wykaż, że |PB|=|PA|+|PC| Widzę, że ∡APB=∡CAB=60 i ∡BPC=∡BAC=60(oparte na tym samym łuku) Piszę z twierdzenia cosinusów dwie równości x²+z²−xz=a²=y²+z²−yz x²−y²=xz−yz (x−y)(x+y)=z(x−y) (x−y)(x+y)−z(x−y)=0 (x−y)(x+y−z)=0 No i co z tym teraz? Bo trochę nad zadaniem nie panuję. Proszę o pomoc i wyjaśnienie

Raf131: Jeżeli y<x albo y>x to dzielisz obustronnie przez (x−y) i wtedy z=x+y Jeżeli y=x to mamy deltoid o bokach x, x, a, a, ale my wiemy o dwóch bokach długości a tego deltoidu i jednej jego przekątnej równej a. Znamy również kąty tej figury 60^o, 90^o, 90^o, 120^o. Wystarczy obliczyć długości boków x oraz przekątną z w zależności od a i pokazać, że z=2x

YushokU: Faktycznie Dziękuję ślicznie, bo mi to nie dawało spokoju