. Ostiii: Ciągi Wyznacz te wartości x, dla których ciąg arytmetyczny o wyrazach:

	y
y−x,		,xy jest malejący.
	x

Proszę o pomoc

Raf131: warunek ciągu malejącego?

Ostiii: a_n<a_n+1 to wiem ale dziwne rzeczy mi wychodzą i się gubię

Ostiii: a_n>a_n+1 ***

Raf131: zobacz tutaj: https://matematykaszkolna.pl/strona/263.html

Ostiii: Znam wzory. Podpunkt a zrobiłem z ciągiem rosnącym, lecz ten podpunkt nie chce mi wyjść.

Ostiii: pomoże ktoś?

Raf131: zaraz się wezmę za to, chociaż ciekawe zadanie, moja idea jest taka, żeby rozważyć kilka przypadków w zależności od x>0, x<0, y>0, y<0 tam chyba jeszcze x>1 oraz x<1 no i x≠0 oraz łatwo zauważyć, że dla y=0, x=1 jedna z nierówności jest sprzeczna

Raf131: zrobiłem to tak, z własności ciągu arytmetycznego:

	an−1 + an+1
an =
	2

	x2
dostajemy zależność y =
	(x−1)(x+2)

następnie wyliczam wyrazy a₁, a₂, a₃ w zależności od samego x, później a₃−a₂ < 0 i moja odpowiedź to x∊(−∞; −2)∪(−1; 0)

Ostiii: Odpowiedz poprawna

Eta:

	y
ciąg y−x,		, xy −−−malejący r<0 i x≠0
	x

	y		y		y		y
r=		−y+x = −		(x−1)+x i r= yx−		=		(x2−1)
	x		x		x		x

	y		y
to		(x2−1)=−		(x−1)+x /*x≠0
	x		x

	x2
y(x−1)(x+2)=x2 ⇒ y=
	(x−1)(x+2)

	y		x2
r<0		(x2−1)<0 ⇒		*(x−1)(x+1)<0
	x		(x−1)(x+2)

x(x+1)
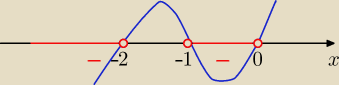
	<0 ⇒ x(x+1)(x+2)<0 ⇒ x∊( −∞, −2) U (−1,0)
x+2

Ostiii: Dziękuję

Eta: