Geometria analityczna Matura2015: Okręgi x²+y²=9 i (x−3)²+(y−3)²=4 przecinają się w punktach P i Q. Oblicz sumę odległości punktów P i Q od początku układu współrzędnych. Próbowałam układem równań i mi źle wyszło, zastanawiam się czy nie ma jakiejś "krótszej" drogi Pomocy

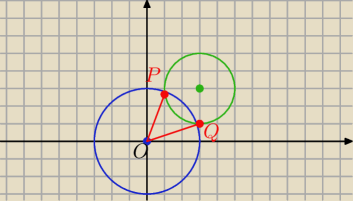
Mila: Okręgi x²+y²=3² i (x−3)²+(y−3)²=2² Dla orientacji rysuję okręgi w ukł. wsp. Punkty P i Q leżą na okręgu o środku (0,0) i promieniu r=3 to ich odległość |OP|=3 i |OQ|=3 Suma odległości wynosi 3+3=6 Nie ma potrzeby liczyć wsp. punktów przecięcia , ale też wyjdzie to samo.

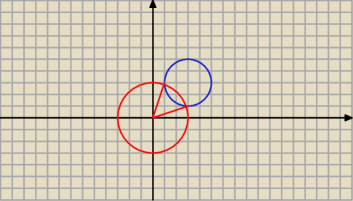
Janek191: x² + y² = 9 r₁ = 3 (x − 3)² + ( y − 3)² = 4 d = r₁ + r₁ = 2*3 = 6 ==================