zadanie Zosia :): Krawędź podstawy prawidłowego ostrosłupa czworokątnego ma długość 10. Kąt pomiędzy sąsiednimi ścianami bocznymi ma miarę 120 stopni. Oblicz pole powierzchni bocznej ostrosłupa.

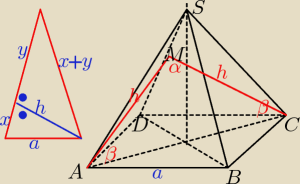
Basia: ponieważ ostrosłup jest prawidłowy ⇒ jego ściany boczne są przystającymi trójkątami równoramiennymi ⇒ wysokości tych ścian wyprowadzone z punktów A i C muszą mieć spodek w tym samym punkcie M i oczywiście tę samą długość ⇒ trójkąt AMC jest równoramienny α=120 b=30 AC = a√2=10√2 bo jest przekątną kwadratu z tw.sinusów

sinα		sinβ
	=
AC		h

sin120		sin 30
	=
10√2		h

√3		1
	=
20√2		2h

2√3*h = 20√2

	√2		10√6
h = 10*		=
	√3		3

x²+h²=a²

	100*6
x2+		=100
	9

	100*2
x2+		= 100
	3

	200		300−200		100
x2 = 100 −		=		=
	3		3		3

	10		10√3
x =		=
	√3		3

y²+h² = (x+y)² y²+h² = x² + 2xy+y² h² = x² + 2xy 2xy = h²−x²

	10√3		100*6		100*3
2*		*y=		−
	3		9		9

20√3		300		100
	*y =		=
3		9		3

	100		3		5		5√3
y =		*		=		=
	3		20√3		√3		3

	10√3		5√3		15√3
x+y =		+		=		= 5√3
	3		3		3

	(x+y)*h
Pściany bocznej =		=
	2

10√6   5√3*   3
	=
2

50√18		50√9*2		50*3√2
	=		=		= 25√2
6		6		6

P_c = P_p+4*P_{ściany bocznej} = 10² + 4*25√2 = 100+100√2 = 100(1+√2) uff, mam nadzieję, że nie pomyliłam się w rachunkach