Pomocy! Kaśka: w trójkacie równoramiennym kat przy podstawie jest α a przy wierzcholku β majac dane ze sin α=15/17.oblicz sin β i cos β z gory dzięki

Basia:

	h		15
sinα=		=		⇒
	c		17

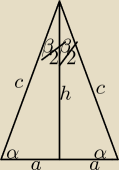
h=15x c=17x a²+h²=c² a² = c²−h² = 17²x²−15²x² = x²(17²−15²) = x²(17−15)(17+15) = x²*2*32 = 64x² a = 8x sin^β₂ = ^a_c = ^8x_17x = ⁸₁₇ cos^β₂ = ^h_c = ^15x_17x = ¹⁵₁₇ sinβ = 2sin^β₂cos^β₂ = 2*⁸₁₇*¹⁵₁₇

	152−82
cosβ = cos2β2 − sin2β2 =
	172

dokończ sobie obliczenia −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− jest też drugi sposób cos^β₂ = ^h_c = sinα = ¹⁵₁₇ sin^β₂ liczymy z wzoru sin^2β₂ + cos^2β₂ = 1 i po wyliczeniu podstawiamy do wzorów sinβ = 2sin^β₂cos^β₂ cosβ = cos^2β₂ − sin^2β₂