przedziały xxxxxxxxxxx:

	2x2−8x+8
Wyznacz maksymalne przedziały monotoniczności funkcji f: f(x)=		.
	x−4

xxxxxxxxxxx: Ktoś może wie jak to rozwiązać?

Janek191:

	2 x2 − 8 x + 8
f(x) =		, x ≠ 4
	x − 4

więc

	(4 x − 8)*( x − 4) − ( 2 x2 − 8 x + 8)*1
f '(x) =		=
	( x − 4)2

	4 x2 − 16 x − 8 x + 32 − 2 x2 + 8 x − 8
=		=
	( x −4)2

	2 x2 − 16 x + 24		2*(x2 − 8 x +12)
=		=
	( x − 4)2		( x − 4)2

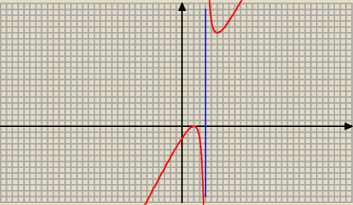
Janek191: f '(x) > 0 ⇔ x² − 8 x + 12 > 0 Δ = 64 −4*1*12 = 64 − 48 = 16 √Δ = 4

	8 − 4		8 + 4
x1 =		= 2 x2 =		= 6
	2		2

f'(x) > 0 ⇔ x ∊ ( −∞ , 2) ∪ ( 6, + ∞ ) oraz f '(x) < 0 ⇔ x ∊ ( 2 , 6 ) \ { 4 } zatem funkcja f rośnie w przedziałach : ( − ∞ , 2) , ( 6 , + ∞), a maleje w przedziałach: ( 2, 4) , ( 4, 6). Patrz też na wykres funkcji f.

Janek191: ?

pigor: ... maksymalne przedziały, to przedziały: "podomykane", czyli tu będą to przedziały : (−∞;2 > oraz < 6;+∞). ...

pigor: ..., a dla f. malejącej będą to przedziały : < 2;4) oraz (4;6 > . ....

xxxxxxxxxxx: Wielkie dzięki!