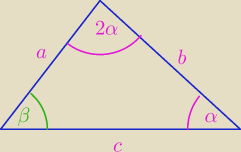
wykaż, że... Maja: Długości dwóch boków trójkąta są równe a i b. Kąt leżący naprzeciwko trzeciego boku jest dwa razy większy od kąta i leżącego naprzeciwko boku o długości a. Wykaż, że długość trzeciego boku wynosi √a(a+b)

agata:

chichi:

	1		1		c
P=		ab*sin(2α)=		bc*sin(α) ⇒ cos(α)=
	2		2		2a

Z tw. Carnota:

	c		bc2
a2=b2+c2−2bc*		⇒ a2=b2+c2−		/ *a
	2a		a

a³=b²a+c²a−bc² ⇒ a³−b²a=(a−b)c² ⇒ a(a−b)(a+b)=(a−b)c² ⇒ c=U{a(a+b)} □

chichi: chochlik c=√a(a+b)*

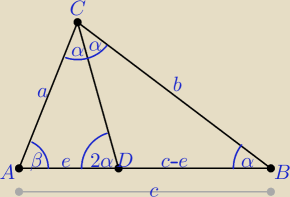
Gucio: Alternatywne rozwiązanie:

	a		b		ac
Na podstawie tw. o dwusiecznej w trójkącie		=		, stąd e =
	e		c − e		a + b

	c		a		a2
ΔABC ∼ ΔADC na podstawie cechy podobieństwa kkk,		=		, stąd e =
	a		e		c

ac		a2
	=		stąd c2 = a(a + b), c = √ a(a + b)
a + b		c

Filip: gucia ROZWIAZANIE lepsze pod KAZDYM wzgledem

Maja: Maja z roku 2021 @ Maja z roku 2015

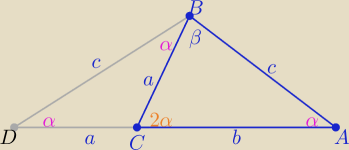
Maja: To jeszcze taki sposób Trójkąty ABC i ABC są równoramienne i podobne z cechy (kkk)

c		a
	=		⇒ c2=a2+ab
a+b		c

to c= √a(a+b) ==========

Maja: Oczywiście miało być : Trójkąty ABD i DBC