Zabawa 5-latek: Do tegorocznych maturzystów W związku z tym ze kochana matura zbliza się wiekimi krokami to może będziecie sami dla siebie pisać przydatne wzory które sa lub nie ma w tablicach matruralnych . Może ja zaczne np. z trygonometrii 1. sin²x+cos²x=1

	sinx
2. tgx=		ale czy dla wszystkich katow ?
	cosx

	cosx
3. ctgx=		to samo pytanie
	sinx

4. tgx* ctgx=1 (dla jakich kątow ?

	1
a z etgo tgx=
	ctgx

	1
5. 1+tg2x}=		a ztego
	cos2x

	1
cos2x=
	1+tg2x

	1
6. 1+ctg2x=		a z tego
	sin2x

	1
sin2x=		Na razie tyle bo muszse jechać do pracy .
	1+ctg2x

Potem jeszcze wpiszse pare wzorow . Wiec się bawcie

Saizou : a worki 5 i 6 pochodzą z wzorów na cos(2x) cos(2x)=cos²x−sin²x=

	2cos2x−1		2cos2x−1
cos2−(1−cos2x)=2cos2x−1=		=		=
	1		sin2x+cos2x

1   cos2x(2− )   cos2x		1   2−   cos2x
	=
sin2x   cos2x( +1)   cos2x		tg2x+1

zatem

	1   2−   cos2x
2cos2x−1=
	tg2x+1

	1   2−   cos2x
tg2x+1=		=
	2cos2x−1

2cos2x−1   cos2x		2cos2x−1		1		1
	=		*		=
2cos2x−1		cos2x		2cos2x−1		cos2x

	1
ostatecznie więc tg2x+1=
	cos2x

a jak już to znamy to pokazanie wzoru 6 jest proste

jakubs: Ja polecam zapoznać się z http://pl.wikipedia.org/wiki/Twierdzenie_Ptolemeusza Czasami przydatne twierdzonko

Saizou : jakubs a jakie twierdzenia w matematyce nie są przydatne ?

pigor: ..., a nie lepiej z jedynki trygonometrycznej np. tak : sin²x+cos²x =1 / : cos²x≠0 (albo przez sin²x≠0) ⇒

	1		1
⇒ tg2+1 =		albo 1+ctg2x =		i koniec kropka .
	cos2x		cos2x

Saizou : też można, jest nawet łatwiej no ale maturzystą trening "obliczeniowy" nie zaszkodzi

Saizou : *grryyy... maturzystom

jakubs: Saizou miałem na myśli pod maturkę, przecież nikt nie będzie się uczył np. tw Bolzano−Weierstrassa na maturę.

Saizou : no niby tak, ale jest to bardzo uzyteczne tw. w matematyce xd

kleszcz: A z podstawy zrobicie? .

Saizou : kleszczu co masz na myśli ?

kyrtap: Moje dwa wzorki nie wiem czy używane: prosta przechodząca przez punkty A = (x₁,y₁) , B =(x₂,y₂) ma postać:

	y2 − y1
y−y1 =		(x − x1)
	x2−x1

Środek okręgu S = (a,b) o postaci ogólnej x2+y2+Ax+By+C=0 i jego promień można wyznaczyć w taki sposób: S :

	⎧	−2A = a
	⎩	−2B = b

r = √a² + b² − C

kleszcz: A wzory, których nie ma w tablicach na przykład na liczbę przekątnych n−kąta.

kyrtap:

	n(n−3)
d =
	2

gdzie d − liczba przekątnych n − liczba kątów

kleszcz: Kurde kyrtap nie wiedziałem, że z postaci ogólnej można obliczyć środek okręgu i promień. Ten wzór na prostą przechodzącą przez dwa punkty jest na karcie wzorów, tylko w jakiejś udziwnionej wersji(ale się już przyzwyczaiłem do tej udziwnionej ).

kleszcz: Ciekawe, czemu te wzory pominęli na karcie wzorów zapomnieli o nich, na przykład na tej karcie wzorów na ma w ogóle zależności w figurach opisanych i wpisanych na okręgu(przykładowo trójkąt równoboczny opisany na okręgu).

kyrtap: aha i jeszcze taka uwaga do tej postaci prostej przechodzącej przez dwa punkty jeśli przykładowo punkty będą miały współrzędne A = (1,5) , B = (1,3) to prosta ta przechodząca przez punkty A i B będzie miała postać x = 1 , analogicznie jeśli A = (0,5) , B = (−2, 5) prosta : y = 5

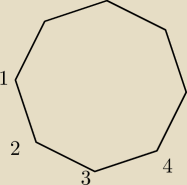
Saizou : wzór na ilość przekątnych można zapamiętać tak że mamy n wierzchołków przekątne na 100% nie "idą" z wierzchołka 2 do wierzchołków 1,2,3, czyli do trzech wierzchołków, dlatego mamy (n−3), takich sytuacji mamy n, bo jest n wierzchołków, wiec n(n−3) jeszcze sprawa dlaczego dzielimy przez dwa, a no dlatego że przekątne 1−4 to to samy co 4−1,

	n(n−3)
wiec została zliczona 2 razy, zatem d=
	2

kyrtap: Saizou wiadomo takie wzorki tylko wyprowadzać, nie warto i wklepywać na dysk jeśli się wie jak wyznaczyć

Saizou : Lepiej napisać dla kogoś kto nie wiem

Saizou : *wie

kyrtap: jeśli jakiś uczeń skorzysta z tego co zapisaliśmy teraz na maturze to jest już sukces dla nas

kleszcz: A jak to było z trójkątem równobocznym wpisanym i opisanym w okrąg − coś tam pamiętam, że była taka zależność, że w którymś R=²₃h, a w innym było r=¹₃h. Tylko teraz co było w czym? . To mi się myli zawsze.

Saizou : co jest dłuższe: promień okręgu wpisanego czy opisanego ?

	2		1
oraz co jest dłuższe		h czy		h
	3		3

kleszcz: Aha, chyba w taki razie Promień okręgu opisanego w trójkąt równoboczny R=²₃h Promień okręgu wpisanego w trójkąt równoboczny r=¹₃h Dobrze piszę?

kyrtap: tak

kyrtap: "Promień okręgu opisanego na trójkącie równobocznym"

Saizou : to było w domyśle

kleszcz: no tak, rzeczywiście dziwnie to napisałem .

kleszcz: A jak był okrąg opisany na kwadracie to promień to była połowa przekątnej kwadratu?. W ogóle coś jeszcze jest ważnego do zapamiętania z tych figur płaskich opisanych i wpisanych, co często i rzadziej zdarza się w zadaniach?.

kleszcz:

5-latek: https://matematykaszkolna.pl/forum/286173.html