planimetria franco: Miary α,β,γ kątów wewnętrznych trójkąta spełniają warunek sinα=2sinβcosγ. Udowodnij, że ten trójkąt jest równoramienny

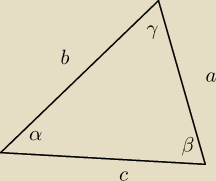
Frost: sinα=2sinβcosγ

a		b		c
	=		=
sinα		sinβ		sinγ

a		b
	=
2sinβcosγ		sinβ

a
	=b
2cosγ

γ=180−(α+β) cosγ=cos(180−(α+β))=−cos(α+β)=sinα*sinβ−cosα*cosβ

franco: Dziękuję

pigor: ..., miary α,β,γ kątów wewnętrznych Δ spełniają warunek sinα=2sinβcosγ. Udowodnij, że ten Δ jest równoramienny ... −−−−−−−−−−−−−−−−−−−−−−−−−−−− ..., a w szufladzie mojej Maji widzę to np. tak : sinα= 2sinβcosγ ⇔ ⇔ sin(180^o−(β+γ))= 2sinβcosγ ⇔ sin(β+γ)= 2sinβcosγ ⇔ ⇔ sinβcosγ+sinγcosβ −2sinβcosγ=0 ⇔ sinγcosβ −sinβcosγ=0 ⇔ ⇔ sin(y−β)= 0 ⇒ γ−β= 0 ⇔ γ=β, c.n.u. . ...

franco: Dziękuję