relacje zbioru kartezjańskiego kuba: zbadaj właściwości relacji R w zb A={0,1,2}: (m,n)∊R ⊂ AxA, jeśli m+n∊A wypisuje punkty spełniające zależność : A`={(0,0),(0,1),(0,2),(1,0),(1,1),(2,0)} i czy pomiędzy wszystkimi puntami muszą zachodzić relacje? bo w takim wypadku wychodzi mi że jest tylko relacja przeciwzwrotności i nie wiem, bo np w relacji symetryczności są punkty (0,1)R(1,0) oraz (0,2)R(2,0), ale zostają punkty (0,0) i (1,1), czyli wtedy po prostu nie jest symetryczna ?

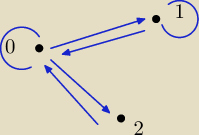
Qulka: Relacja NIE jest zwrotna JEST symetryczna NIE jest przechodnia

kuba: chyba rozumiem, dziekuje