zadanie Blue: Miara kąta między ścianami bocznymi ostrosłupa prawidłowego czworokątnego wynosi β. Wykaż, że cosinus kąta między ścianą boczną tego ostrosłupa a jego podstawą jest równy √−cosβ. Błagam o pomoc, robię różne przekształcenia, z tw. cosinusów, trójkątów podobnych i nic mi nie wychodzi

Kacper:

===:

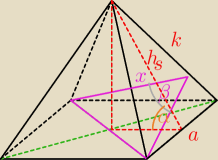
	x		1
(a√2)2=x2+x2−2x2cosβ ⇒		=
	a		√1−cosβ

	x		hs		hs
Zauważ trójkąty podobne i zależność		=		=
	a		k		√hs2+a2/4

	1		2hs
		=
	√1−cosβ		√4hs2+a2

	a2
4hs2+a2=4hs2−4hs2cosβ ⇒ a2=−4hs2cosβ hs=√
	−4cosβ

	a		a
cosα=		=		=√−cosβ
	2hs		a2   2√   −4cosβ

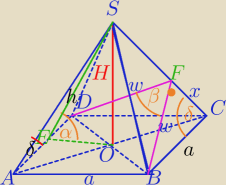Mila: ES=h

	12a
cosα=
	h

========= W ΔDBF: (a√2)²=w²+w²−2w²cosβ

	a2		a
w2=		⇔w=
	1−cosβ		√1−cosβ

W ΔBFC: x²+w²=a² x²=a²−w²

	a2
x2=a2−
	1−cosβ

	a2*(−cosβ
x2=
	(1−cosβ)

	a√−cosβ
x=		, β− kat rozwarty
	√1−cosβ

W ΔBFC:

	x		a√−cosβ		√1−cosβ
ctgδ=		=		*
	w		√1−cosβ		a

ctgδ=√−cosβ W ΔAES:

	12a
ctgδ=		=cosα=√−cosβ
	h

cnw ==========

Blue: Dzięki serdeczne Wam

Mila: :