 proszę o sprawdzenie i wytłumaczenie błędów oraz zadań 6 i 7
1. Zbiorem rozwiązań nierówności ax − 6 < 0 z niewiadomą x jest przedział (− 3,+ ∞ ) .
Wyznacz a .
z tego wynika,że x ∊ (− 3,+ ∞ )
−3a − 6 = 0
a = −2
spr −2x − 6 < 0 , x > −3
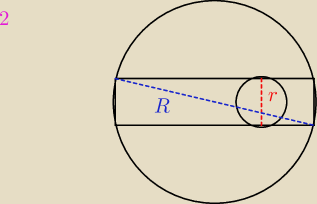
2. Prostokąt jest wpisany w okrąg o promieniu 10, a jego dłuższe boki są styczne do okręgu
o promieniu 3.Oblicz pole.
2r = a
6 = a
R = 10 = d
d = √a + b2
10 = √a2 + b2
100 = 36 + b2
b = 8
P = 6*8 = 48
3. Uzasadnij, że jeżeli liczba całkowita n nie dzieli się przez 5, to 4 n daje przy
dzieleniu przez 5 resztę 1.
(5n+1)4 = (5n+1)2*(5n+1)2 = 625n4 + 500n3 + 150n2 + 20n +1
5(125n4+ 100n3 + 30n2 + 4n) + 1
4. Ewa na początku 2015 roku kupiła skarbonkę i włożyła do niej 1000 zł. Na początku każdego
kolejnego roku Ewa dokłada do skarbonki kwotę równą 20% dotychczas zgromadzonych oszczędności,
a przez resztę roku nie dokłada, ani nie wybiera ze skarbonki żadnych pieniędzy. Ile będą
wynosić oszczędności Ewy pod koniec roku 2020?
proszę o sprawdzenie i wytłumaczenie błędów oraz zadań 6 i 7
1. Zbiorem rozwiązań nierówności ax − 6 < 0 z niewiadomą x jest przedział (− 3,+ ∞ ) .
Wyznacz a .
z tego wynika,że x ∊ (− 3,+ ∞ )
−3a − 6 = 0
a = −2
spr −2x − 6 < 0 , x > −3
2. Prostokąt jest wpisany w okrąg o promieniu 10, a jego dłuższe boki są styczne do okręgu
o promieniu 3.Oblicz pole.
2r = a
6 = a
R = 10 = d
d = √a + b2
10 = √a2 + b2
100 = 36 + b2
b = 8
P = 6*8 = 48
3. Uzasadnij, że jeżeli liczba całkowita n nie dzieli się przez 5, to 4 n daje przy
dzieleniu przez 5 resztę 1.
(5n+1)4 = (5n+1)2*(5n+1)2 = 625n4 + 500n3 + 150n2 + 20n +1
5(125n4+ 100n3 + 30n2 + 4n) + 1
4. Ewa na początku 2015 roku kupiła skarbonkę i włożyła do niej 1000 zł. Na początku każdego
kolejnego roku Ewa dokłada do skarbonki kwotę równą 20% dotychczas zgromadzonych oszczędności,
a przez resztę roku nie dokłada, ani nie wybiera ze skarbonki żadnych pieniędzy. Ile będą
wynosić oszczędności Ewy pod koniec roku 2020?
| 1 | ||
1000 * | = 200 | |
| 5 |
| 1 | ||
1200 * | = 240 | |
| 5 |
| 1 | ||
1440 * | = 288 | |
| 5 |
| 1 | ||
1728 * | = 345,6 | |
| 5 |
| 1 | ||
2073,6 * | = 414,72 | |
| 5 |
| ah | ah | ||
= 6 | = 24 | ||
| 2 | 2 |
| bh | |
= 24 | |
| 2 |
| 1 | ||
PABC = | *AC*hb | |
| 2 |
| 1 | ||
1458 = | r2h | |
| 3 |