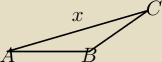
Oblicz dlugość odcinka x Damian: Na rysunku niestety nie dalo sie opisac... AB = {3} BC = 3{3} Kąt przy B jest rowny 150 stopni Skorzystalem z twierdzenia cosinusow: x²= {3}²+(3{3}²−2*{3}*3{3}*(−{3}/2) x²=3+27−9{3} Jak narazie jest ok czy gdzies poknocilem?

5-latek : Damian Masz tam kolo tej linijki (WPISZ A OTRZYMASZ wiec to zrob Potem sprawdze I zapisujemy tak x²= AB²+BC²− itd (najpierw symbolami a potem wstawiamy obliczenia

Damian: Wiem jak wpisywac, ale przy rysowaniu nie da sie pisac znakow.

Damian: x²= AB²+BC² − 2AB*BC*cos150 cos150−−> cos(1*90+60)= −sin60= −√3/2 x²=√3²+3√3²−2*√3*3√3*(−√3/2) x²=3+27−18*(−√3/2) x²=30+9√3

5-latek : Zrobiles Damian blad w zapisie otoz 3√3²= 9 a nie 27 Powinienes zapisac to tak x²=√3²+(3√3)2− dalej dobrze bo (3√3)²= 3³*(√3)²=9*3=27 ze wzoru (a*b)ⁿ= aⁿ* bⁿ x²=30+9√3to x= √30+9√3 lub x=−√30+9√3 ale x ma byc >0 bo to bok wiec x= √30+9√3 Teraz to co pod pierwiastkiem zwin do pelnego kwadratu z ewzoru skroconego mnozeia