Wykaz, ze trojkat jest prostokatny i oblicz obwod Daniel: Wykaz ze trojkat PQR jest prostokatny i oblicz jego obwod P=(−4,−6) Q=(2,5) R=(−2,4) Niech mi ktos rowiaze te zadanie wraz z tlumaczeniem, a pozniej niech mi ta osoba poda jakies 3 inne punkty i sprobuje to sam obliczyc... Bardzo Prosze

J: to może na początek sam oblicz długości boków

Daniel: Czyli mam policzyc punkty PQ , PR i QR ze wzoru (x2−x1)² + (y2−y1)² wszystko pod pierwiastkiem?

J: dokładnie tak

Daniel: PQ= pierwiastek z 157 PR= pierwiastek z 104 QR= pierwiastek z 17 Dobrze?

kix: 104 źle

J: policzone dobrze, ale to nie jest trójkąt prostokątny , sprawdź treść zadania

kix: sorki, dobrze

Daniel: Nie rozumiem o co chodzi

J: ten trójkąt nie jest prostokątny

kix: tak jak J napisał, policzyłeś dobrze długości boków, lecz nie jest to Δ prostokątny

Daniel: Czyli to koniec zadania czy jak? Po prostu mam napisac, to nie jest trojkat prostokatny i tyle? Czy jeszcze cos z obwodem trzeba zrobic?

J: policz obwód i dopisz,że ten trójkąt nie jest prostokątny ( jesli dobrze przepisałeś treść zadania )

kix: dokładnie tak możesz napisać, ale masz jeszcze obliczyć jego obwód

Daniel: Tresc na pewno dobrze przepisana ObwΔ= pierwiastek z 157 + pierwiastek z 104 + pierwiastek z 17 = pierwiastek z 278 Trojkat nie jest prostokatny i to jest koniec zadania tak?

J: Katastrofa ! √a + √b + √c ≠ √a+b+c !

kix: liczby podpierwiastkowe nie sumuj pod jednym pierwiastkiem

Daniel: hmmmm?

Daniel: Przeciez nie sumuje ;s √157 + √104 + √17 = √278 ?

kix: obwód będzie sumą poszczególnych pierwiastków

kix: trzy posty wyżej J napisał przecież że takie działanie jest zabronione

Daniel: Czyli jak dokladnie ma to wygladac?

kix: Ob = √157 + √104 + √17

Daniel: i tak ma zostac, nie sumowac tego tak?

J: możesz jeszcze: √104 = √4*26 = 2√26

kix: zostaw tak jak jest, będzie GUT

Daniel: Ale to chyba lepiej napisac tak jak napisal kix, co nie ? Przeciez tak tez moze chyba byc Mam jeszcze kilka zadan, pomoglibyscie rozwiazac?

kix: zapis zaproponowany przez J jest z matematycznego punktu widzenia bardziej elegantisze

Daniel: Mam jutro poprawe sprawdzianu i chcialbym go zdac :s A sam nie dam rady tego ogarnac, w sumie mam rozwiazane po troszku te zadania i chcialbym sie was zapytac czy to dobrze jest

kix: pisz, jak ktoś będzie miał czas to z pewnością pomoże

Daniel: Okej, to po kolei. Sprawdz czy punkty PML leza na jednej prostej [czy sa wspoliniowe] P=(2,0 M=(0,−1) L=(4,2) i ja to zrobilem tak, wzialem punkty PM i obliczylem prosta ze wzoru (x2−x1)(y−y1)=(y2−y1)(x−x1) Prosta mi wyszla y=1/2x−1 nastepnie podstawilem z punktu L 4 za x i mi wyszlo. y=1/2*4−1=2−1=1≠2 prostej MP /// i napisalem ,ze nie sa wspoliniowe dobrze, jest to zrobione?

J: za dużo roboty ... wystarczy sprawdzić same współczynniki kierunkowe prostych

	0−2
PM: a =		= 2
	−1 − 0

	4−2
PL: a =		= 2
	2−0

PLM są współliniowe

Daniel: To ja tez cos zle zrobilem ,bo mi wyszly, ze nie sa wspoliniowe a Tobie ze sa ;s... a mozesz podac wzor na to jak Ty to obliczyles?

J: wspólczynnik kierunkowy prostej przechodzącej przez punkty A i B :

	yB − yA
a =
	xB − xA

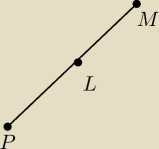
J: jeśli proste: PL i PM mają taki sam wspólczynnik kierunkowy, to PLM są współliniowe

kix: współczynniki kierunkowe mogą się zgadzać, lecz mogą się różnić o wyraz wolny i wtedy nie będą się proste pokrywały

Daniel: I to jest koniec zadania?

kix: nie, napisałem to w kontekście tego co kolega J podał o współczynnikach kierunkowych, a twoje punkty nie są współliniowe − w prosty sposób możesz sprawdzić swoje obliczenia nanosząc współrzędne tych punktów na wykres

kix: czyli zrobiłeś dobrze

Daniel: Czyli co teraz musze zrobic?

kix: w odpowiedzi napiszesz, że nie są współliniowe

J: @kix .. zastanów się, co napisałeś i popatrz na rysunek , jesli proste PL i PM maja taki sam współczynnik kierunkowy i obie przechodzą przez punkt P to muszą się pokrywać

J: nie ściemniaj , bo są wspólniniowe

Daniel: Kurcze juz sie potracilem w tym

kix: @J wszystko byłoby OK gdyby punk L leżał pomiędzy M i P , a tak nie jest

J: teraz to ja ściemniłem ... sorry

kix: @Daniel, pomyłki się zdarzają, dobrze zrobiłeś i nie załamuj się , dawaj dalej

kix: @J taki urok pracy na kilku frontach

J: racja , myślami jestem przy innym zadaniu

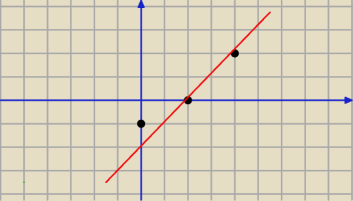
5-latek : Daniel przeciez w innym poscie (troche czasu temu Mila Ci pokazala jak to sprawdzic

Daniel: Czyli te moje obliczenia sa dobre tak? Ok... A odp to punkty PML nie sa wspoliniowe teraz 2 zadanie Wiedzac, ze punkt M jest srodkiem odcinka AB wyznacz wspolrzedne punktu B A=(3,4) M=(1,7) zrobilem to tak xa+xb/2 ya+yb/2=S(a,b) 3+xb/2 4+yb/2=(1,7) 3+xb/2=1/*2 4+yb/2=7/*2 3+xb=2 4+yb=14 xb=2−3 yb=14−4 xb=−1 yb=10 i odpowiedz B=(−1,10) dobrze?

5-latek : Poniwaz jest to zadnie z geometrii analitycznej robimy to tak Rysujemy odcinek AB i na min zaznaczamy punkt M Teraz juz widzimy co mamay robic

	xA+xB
xM=		to 2xM= xA+xB to xB= 2xM−xA
	2

To samo y_M= .....

Daniel: a nie moge zrobic tak jak ja zrobilem?

kix: wynik masz dobry, a klasyczną metodę podał 5−latek

J: zrobiłeś tak samo i dobrze policzyłeś

Daniel: Dobra, czyli 3 zadania mam z glowy W sumie ostatnie teraz. Okresl wzajemne polozenie dwoch okregow o rownaniach (x+2)² + (y−2)²=64 i x²+y²−4x+2y−4=0 Tu nie mam pojecia co zrobic;c

5-latek : Wiesz mnie kiedys uczona ze nawet do najprostszsego zadania z geometrii analitycznej nalezy zrobic rysunek (chyba ze to wyraznie zaznaczono ze bez rysunku

kix: drugie równanie okręgu zapisz w takiej postaci jak jest zapisane pierwsze

J: Policz promienie tych okręgów

5-latek : 1. Odczytaj srodek i promien okregu z 1 rownania i narysuj go w ukladzie wspolrzednych 2 Rownanie nr 2 doprowadz do postaci kanonicznej i odczytaj z niego srodek i promien i tak samo narysuj go w ukladzie wspolrzednych

Daniel: S=(−2,+2) r=8 z tego pierwszego rownania a co dalej? ;s

kix: a teraz drugie równanie okręgu sprowadź do takiej samej postaci jak równanie pierwszego

5-latek : Otoz tez jesli masz rownanie okregu w postaci ogolnej (zredukowanej czyli x²+y²+Ax+By+C=0 to z tej postaci rowniez mozesz odczytac srodek okregu i promien

	A		B		√A2+B2−4C
xsr= −		ysr= −		i promien r=
	2		2		2

Patrzysz na rownanie i jesli A²+B²−4C>0 to to jest rownanie okregu

5-latek : Warto jest znac 2 metody

Daniel: Chyba sobie odpuszcze to zadanie, bo ciezko je kumam Dziekuje za pomoc mi w zadaniach

kix: lepiej niech się nauczy sprowadzać równanie to klasycznej postaci (x−a)²+(y−b)²=R²

kix: x²+y²−4x+2y−4 = (x−2)²+(y+1)²=9

5-latek : Jeszce bede chwile to sprobujemy to zrobic Masz takie rownanie okregu x²+y²−4x+2y−4=0 KOrzystamy z e wzorow skroconego mnozenia \(a+b)²= a²+2ab+b² lub (a−b)²= a²+2ab+b² Teraz popatrz Mamy x²−4x wiec skorzystamy z e wzoru (a−b)²=a²−2ab+b² zobacz (x−2)²= x²−4x+16 Tak? ale my musimy mie tylko x²−4x x²−4x= (x−2)²−16 (musimy ta 16 odjac zeby dostac to samo Teraz mamy y²+2y (korzystamy z ewzoru (a+b)²= a²+2ab+b² Poatrz (y+1)²= y²+2y+2 ale my mamy miec y²+2y wiec od (y+1)² odejmujemy 2 i dostajemy y²+2y bo y²+2y=(y+1)²−2 Mamy to rownanie (zapisze jes troche inaczej zeby bylo lepiej widac x²−4x+y²+2y−4=0 Teraz do tego rownania za x²−4x wstawiamy (x−2)²−4 a za y²+2y wstawiamy (y+1)²−2 (x−2)²−4+(y+1)²−2−4=0 postac kanoniczna jest taka ( (x−x_s)²+(y−y_s)²=r² Wiec nasza postac zielona zapiszsemy tak (x−2)²+(y+1)²= 4+2+4 (x−2)²+(y+1)²=10 Odczytaj z niego srodek i promien i mozesz sobie tez porownac wyniki (zrob sobie obliczenia z postu 11:42

kix: wstawiamy (y+1)²−1 a nie (y+1)²−2

5-latek : Nie wiem o czym mysle ale przeciez (y+1)²= y²+2y+1 ( a nie +2 Popraw to sobie i wszedzie tam gdzie jest odjac 2 popraw na odjac 1 Rownanie bedzie takie jak napisal kolega post 11:58 czyli (x−2)²+(y+1)²=9 Dobrze ze kolego napisales (a ja takiego babola strzelilem

Daniel: Okej, zaraz to sobie przeloze na swoje Dzieki

5-latek : I sprobuj soebie zrobic tak samo takie rownanie x²+y²−6x+2y+6=0

Daniel: Hmm, ciezkie to troszke

kix: wszystko jest trudne zanim stanie się łatwe

5-latek : Zadne to nie jest ciezkie np mamy ten wzor (x−b)²= x²− 2xb +b² patrz na to czerowne Mamy teraz tak (x− no wlasnie ile ?)² zeby dostac x²−6x Zobacz ze w tym wzorze 2xb= 6x teraz przez ile nalezy popnozyc 2 zeby dostac 6? i to jest nasze b