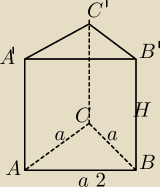
Graniastosłupy Luiza: 1. Krawędź podstawy graniastosłupa prawidłowego trójkątnego ma długość 2, a jego pole powierzchni całkowitej jest równe 36. Oblicz objętość tego graniastosłupa. 2. Oblicz objętość i pole powierzchni całkowitej graniastosłupa prawidłowego czworokątnego o przekątnej ściany bocznej równej 6cm, jeżeli ta przekątna z krawędzią podstawy tworzy kąt 45 stopni.

Baklazan: 1. Podstawą tego graniastosłupa jest trojkat rownoboczny, majac jego bok jestes w stanie policzyc jego pole. Nastepnie ze wzoru na pole graniastoslupa wyznaczasz wysokosci scian bocznych. Nastepnie mając wysokość sciany bocznej i wykorzystując wiedzę gdzie spada wysokośc graniastoslupa trojkatnego prawidlowego obliczasz wysokosc calego graniastoslupa. Teraz zostaje tylko podstawienie pod wzor na objetosc

Mila:

	22√3
PΔABC=		=√3
	4

P_c=2*√3+3*a*H 2√3+3*2*H=36 /:2 √3+3H=18 3H=18−√3

	18−√3
H=
	3

V=P_ΔABC*H

	18−√3
V=√3*
	3

	18√3−3
V=		⇔
	3

V=6√3−1 ========== spr. P_b=3*a*H=a*3H=2*(18−√3)=36−2√3 P_c=36−2√3+2*√3=36 zgodność.