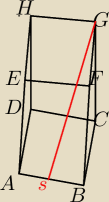
Stereometria. Graniastosłup vdmath: Kwadrat ABCD jest podstawą graniastosłupa ABCDEFGH. Odcinek łączący środek S krawędzi podstawy AB z wierzchołkiem G ma długość d, a prosta SG jest nachylona do płaszczyzny DCGH pod kątem o mierze α. Wyznacz pole powierzchni bocznej prostopadłościanu. Wybaczcie brzydki rysunek Bardzo proszę o pomoc.

kix: narysuj odcinek SC i oblicz jego długość

vdmath:

	a√5
nie wiem czy dobrze, ale wychodzi mi
	2

Eta: P_b=4a*H

	a2		a√5
z tw. Pitagorasa w trójkącie SBC : |SC|= √a2+		=
	4		2

H		|SC|
	=sinα ⇒ H=d*sinα i		= cosα ⇒ |SC|=d*cosα
d		d

	a√5		2d√5
|SC|=		⇒ a√5= 2d*cosα ⇒ a=		*cosα
	2		5

P_b= ........

vdmath: kurcze... ale α miała być od SG do ściany CDGH i nie wiem jak go zaznaczyc

kix: Pani Eta zaznaczyła ten kąt na ślicznym rysunku

vdmath: a ta α z rysunku nie jest do podstawy ABCD?

Eta: Sorry źle odczytałam treść

vdmath: Nic się nie stało, głowię się już 2h i nie wiem jak zaznaczyć ten kąt zwłaszcza, że w podpowiedziach do zadania mam, że krawędź podstawy wynosi dsinα, a mi ni w ząb nie wychodzi

vdmath: Dasz radę to jakoś zaznaczyć? Bo ja już nie wiem

Eta: Zaraz Ci narysuję ..... tylko zrobię herbatę

Eta:

Eta: Bardzo mnie to wkurza .........

Lukas: ?

vdmath: Rysuję... rysuję... i nie mogę znaleźć tego kąta szok Wybacz, ale wczoraj już musiałam to odłożyć.... Masz jeszcze ochotę podzielić się rysunkiem?