Styczna do wykresu funkcji - pochodna karteczka: Wyznacz równanie stycznej do wykresu funkcji f w punkcie P, jeśli:

	4x+2
f(x)=		, P(xo,2)
	x+3

	4(x+3)−1(4x+2)		10
f'(x)=		=
	(x+3)2		(x+3)2

co dalej?

5-latek : rownanie jest takie y=f'(x₀)(x−x₀)+f(x₀)

Braun: https://www.youtube.com/watch?v=VB8VZPEmkL4

karteczka: a jak obliczyć x_o?

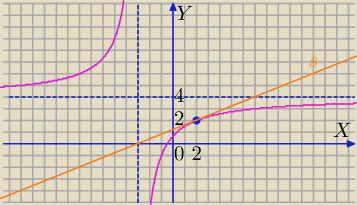
Mila: 1) Punkt styczności

4x+2
	=2 i x≠−3
x+3

4x+2=2(x+3) 4x+2=2x+6 2x=4 x=2 P=(2,2)− punkt styczności 2) Pochodna f(x)

	4*(x+3)−(4x+2)*1
f'(x)=		⇔
	(x+3)2

	10
f' (x)=
	(x+3)2

	10		10		2
f'(2)=		=		=
	(2+3)2		25		5

y=f'(2) x+b, P∊stycznej

	2		2
y=		x+b i 2=		*2+b
	5		5

2−⁴₅=b

	6
b=
	5

	2		6
s: y=		x+
	5		5

================

karteczka: Dziękuję bardzo

Mila: