Z parametrem
milo: Mam problem z jednym zadaniem. Mam wyznaczyć dla jakich wartości parametru m równanie
(m−5)x2 − 3mx + m = 0 ma dwa pierwiastki rzeczywiste z których jeden jest mniejszy a drugi
większy od −1. Wyznaczylem juz Δ i przypadek liniowy rozpatrzylem i wyszlo mi ze m∊(−∞,−4) ∪
(0,∞) \ {5}. Ale co dalej z tymi pierwiastkami?
24 mar 18:38
prosta:
to oznacza, że liczby x1+1 oraz x2+1 są przeciwnych znaków...a stąd
(x1+1)(x2+1)<0
x1x2+(x1+x2)+1<0
24 mar 18:44
Tadeusz:
...wcale nie oznacza
24 mar 18:46
Tadeusz:
a nie łatwiej rozpatrzyć
f(−1) dla m−5>0 i f(−1) dla m−5<0
24 mar 18:48
milo: Tadeuszu moglbys wyjasnic ?
24 mar 18:53
Tadeusz:
tak jak prosta ,,, też można
24 mar 18:57
milo: A jestem ciekaw twojego pomyslu mozna go poznać ?
24 mar 18:59
Tadeusz:
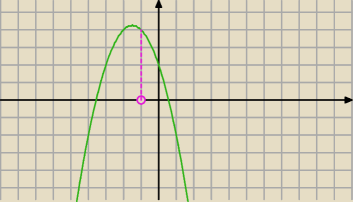
dla m−5<0
24 mar 19:00
Tadeusz:
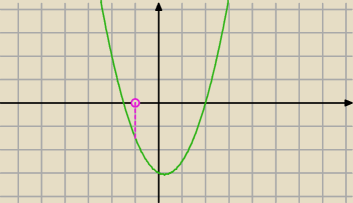
dla m−5>0
24 mar 19:04
milo: Sorry ale kompletnie nic z tego nie rozumiem :'(
24 mar 19:04
milo: Dlaczego akurat m−5>0 i m−5<0

?
24 mar 19:06
Tadeusz:
dla m−5<0 f(−1)>0
dla m−5>0 f(−1)<0
24 mar 19:06
prosta: w metodzie z wykresami trzeba rozpatrywać dwa przypadki(i odwoływać się do wykresu funkcji)..
w moim rozwiązaniu wszystko mamy w jednej nierówności...co jest dość wygodne

24 mar 19:13
Tadeusz:
... każda pliszka ... −

24 mar 20:35
 dla m−5<0
dla m−5<0
 dla m−5>0
dla m−5>0
 ?
?

