stereometria
Blue: w ostrosłupie prawidłowym czworokątnym pole podstawy jest równe S, a kąt między ścianą boczną a
podstawą jest równy α. Ostrosłup ten przecięto płaszczyzną zawierającą krawędź boczną oraz
środek krawędzi podstawy. Oblicz pole otrzymanego przekroju.

24 mar 17:42
Janek191:
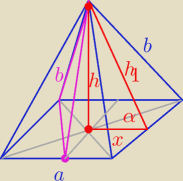
S = a
2 ⇒ a =
√S
x = 0,5 a
24 mar 18:03
Blue: ale właśnie mam problem z wyznaczeniem wysokości przekroju...
24 mar 18:09
Kacper: A czy musisz mieć wysokość, żeby policzyć pole trójkąta?
24 mar 18:19
Blue: Kacper, jak ja Ciebie dawno nie widziałam

No nie muszę, ale w takim razie jakiś sinus kąta by się przydał...
Ej, czekaj, już chyba mam trop!
24 mar 18:35
Blue: Nie , jednak, coś mi nie wychodzi... może jeszcze jakaś podpowiedź?
24 mar 18:44
prosta: jakoś opisać długości boków przekroju ...uzależnić od a...
24 mar 18:47
prosta: są to : b, h1 oraz 0,5a√5
24 mar 18:49
prosta: jeśli oznaczymy x=0,5a to można obliczyć długość podstawy przekroju: x√5
oraz długość wysokości opuszczonej na tę podstawę....z trójkąta zawierającego wysokość bryły
i odcinek poprowadzony ze spodka wysokości ostrosłupa prostopadle do odcinka długości x√5
24 mar 18:57
prosta: h − wysokość przekroju poprowadzona z wierzchołka ostrosłupa
| | x2√10√tg2α+1 | | S√10√tg2α+1 | |
PΔ= |
| = |
| |
| | 8 | | 8 | |
24 mar 19:08
prosta: trzeba poprawić ostatnia linijkę, bo 4x2=S
24 mar 19:10
Blue: | | 1 | |
skąd wiesz, że tam jest |
| przekątnej   |
| | 8 | |
24 mar 19:19
Blue: | | x | |
a tam nie powinno być czasem, że h2= H2+ ( |
| ) 2 |
| | √5 | |
24 mar 19:57
Blue: Dzięki prosta, bo naprowadziłaś mnie na dobre rozwiązanie

Ale będzie tak jak mówię to
tw.Pitagorasa, bo wyszło mi tak jak w odp

24 mar 20:04
Blue: | | S√5−4cos2α | |
Napiszę odp., jakby ktoś chciał wiedzieć: |
| |
| | 8cosα | |
24 mar 20:05
24 mar 20:10
prosta: a dlaczego z cosinusem a nie tangensem.....

?
24 mar 20:11
24 mar 20:17
Blue: bo tak jest w odp.

Ale z tg też by mogło być

24 mar 20:19
Benny: | | x | |
Czemu tam ma być |
| bo jakoś nie mogę tego zobaczyć  |
| | √5 | |
24 mar 20:19
Benny: wróć tu ktoś

24 mar 20:53
Mila:
To nie skończone to zadanie?
24 mar 21:04
Benny: | | x | |
Skończone, ale tak patrze na ten rysunek i nie widzę tego |
| |
| | √5 | |
24 mar 21:05
prosta:
24 mar 22:01
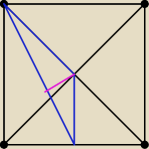
prosta: najdłuższy bok "niebieskiego" trójkąta: x
√5
pole " niebieskiego trójkata: 0,5x
2
| | x | |
wysokość na najdłuższy bok: |
| |
| | √5 | |
24 mar 22:04
Raf131:
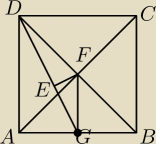
Albo tak:
|DG| − podstawa przekroju.
∡DEF = kąt prosty
|AB| = a
|FG| =
12a
| | a√5 | |
|DG| = √(0.5a)2 + a2 = |
| |
| | 2 | |
| | 3π | | a√2 | | a√5 | |
PDFG = 12 * sin |
| * |
| * 12a = 12 * |EF| * |
| |
| | 4 | | 2 | | 2 | |
Wiedząc, że h =
12 a tgα mamy wysokość przekroju równą
w =
√h2 + |EF|2 =
a2 √(tg α)2 + 1/5
i ostatecznie pole przekroju:
| | a√5 | |
P = 12 * w * |DG| = 12 * a2 √(tg α)2 + 1/5 * |
| = |
| | 2 | |
| | a2 | | S | |
= |
| √5tg2 α + 1 = |
| √5tg2 α + 1 |
| | 8 | | 8 | |
24 mar 22:11

 S = a2 ⇒ a = √S
x = 0,5 a
S = a2 ⇒ a = √S
x = 0,5 a
 No nie muszę, ale w takim razie jakiś sinus kąta by się przydał...
Ej, czekaj, już chyba mam trop!
No nie muszę, ale w takim razie jakiś sinus kąta by się przydał...
Ej, czekaj, już chyba mam trop!



 Ale będzie tak jak mówię to
tw.Pitagorasa, bo wyszło mi tak jak w odp
Ale będzie tak jak mówię to
tw.Pitagorasa, bo wyszło mi tak jak w odp 


 ?
?
 Ale z tg też by mogło być
Ale z tg też by mogło być 



 Albo tak:
|DG| − podstawa przekroju.
∡DEF = kąt prosty
Albo tak:
|DG| − podstawa przekroju.
∡DEF = kąt prosty