Rachunek różniczkowy 3rdpitch: 1. Uzasadnij, że każdy punkt paraboli y=1/2x2 jest oddalony o conajmniej √7 od punktu M=(0,4) Obliczyłem pochodną zmiennej x, wyszły mi dwa min x=√6 i x=−√6 nie wiem czy dobrze/co dalej? 2. Wyznacz najmniejszą wartość jaką może przyjąć suma odwrotności pierwiastków równania x2−8x+k2+4=0 Robiłem to z wzorów vieta, pochodna z 8/k2+4 wychodzi w liczniku −16k, przyrównując to do zera k=0, a dla k=0 wartość początowa równa się 2, w odpowiedziach jest 1/2. 3. Uzasadnij, że równanie x3−x2−5x+3=0 ma trzy pierwiastki rzeczywiste. Tutaj zupełnie nie wiem jak się za to zabrać. 4. Wyznacz te wartości m dla ktorych rownanie x3−3x=m ma trzy rozwiązania. 5. Z drutu o długości 1m zbuduj trójkąt prostokątny o możliwie największym polu. Znajdź długości boków tego trójkąta. 6. Wyznacz zbiór wartości funkcji f(x)=x+6/x gdzie xeR−{0} Obliczyłem pochodną, ekstrema to −√6 i √6, Liczę f(−√6) i f(√6) i wychodzi −2√6 i 2√6 Dlaczego ZW to nie <2√6,−2√6> tylko od zaczyna się od −niesk?

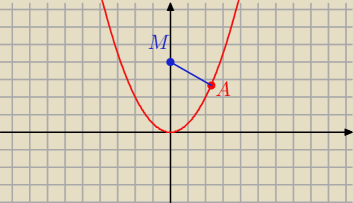
Janek191: z.1 y = 0,5 x² M = ( 0, 4) Mamy A = ( x , 0,5 x²) Liczymy odległość I AM I → AM = [ 0 − x , 4 − 0,5 x²] = [ − x , 4 − 0,5 x² ] więc I AM I = √ x² + ( 4 − 0,5 x²)² = √x² + 16 − 4 x² + 0,25 x⁴ = √ 0,25 x⁴ − 3 x² + 16 Ta odległość będzie najmniejsza, gdy 0,25 x⁴ − 3 x² + 16 osiągnie minimum. f(x) = 0,25 x⁴ − 3 x² + 16 f '( x) = x³ − 6 x = x*( x² − 6) = 0 ⇔ x = 0 lub x = √6 f '' (x) = 3 x² − 6 f ''( √6) = 3*6 − 6 > 0 więc funkcja f osiąga minimum dla x = √6 Wtedy ta odległość jest równa: I AM I = √ 0,25*(√6)⁴ − 3*(√6)² + 16 = √ 9 − 18 + 16 = √7 Dlatego odległość między punktem M a dowolnym punktem danej paraboli nie może być mniejsza od √7.

3rdpitch: dzięki, ktoś coś jeszcze?

Jacek: A mogę zapytać Janek191 czemu to jaki ma znak f'' ma znaczenie, że dla x=√6, f osiąga minimum? Druga pochodna opisze gdzie mamy punkty przegięcia i tyle.

Janek191: x³ − x² − 5 x + 3 = 0 Niech f(x) = x³ − x² − 5 x + 3 więc

	5
f '(x) = 3 x2 − 2 x − 5 = 3*( x + 1)*( x −		)
	3

Δ = 4 − 4*3*(−5) = 4 + 60 = 64 √Δ = 8

	2 − 8		2 + 8		10		5
x1 =		= − 1 x2 =		=		=
	6		6		6		3

	5
f '(x) > 0 ⇔ x ∊ (− ∞ , − 1) ∪ (		, + ∞)
	3

oraz

	5
f '(x) < 0 ⇔ x ∊ ( − 1 ,		)
	3

zatem funkcja f rośnie w ( − ∞ , − 1) , więc musi przeciąć oś OX,

	5
f maleje w ( − 1,		) , więc musi przeciąć oś OX, oraz
	3

	5
znowu f rośnie w (		, + ∞ )
	3

W x 1 = − 1 jest f'( − 1) = 0 − max lokalne

	5
W x 2 =		jest f'(U{5}{3]) = 0 − min lokalne
	3

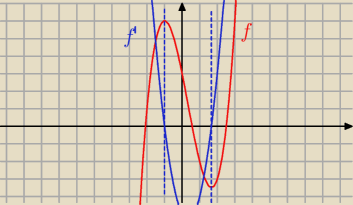
Wykres f trzy razy przecina oś OX , więc równanie ma trzy pierwiastki rzeczywiste. Patrz też na wykresy funkcji f i f ' .

Janek191: z.5 x + y + z = 1 ⇒ z = 1 − x − y x² + y² = z² x² + y² = ( 1 − x − y)² x² + y² = 1 − 2*( x + y) + x² + 2 x y + y² 0 = 1 − 2 x − 2 y + 2 x*y 2 x − 1 = 2 x*y − 2 y 2 x − 1 = 2y*( x − 1)

	2 x − 1
2y =
	x − 1

	x − 0,5
y =
	x − 1

zatem

	x − 0,5
P= 0,5 x*y = 0,5 x*
	x − 1

	0,5 x2 − 0,25 x
P(x) =
	x − 1

	x*( x − 1) − ( 0,5 x2 − 0,25)*1
P '(x) =
	( x − 1)2

	0,5 x2 − x + 0,25
P '(x) =		= 0 ⇔ 0,5 x2 − x + 0,25 = 0
	( x − 1)2

	1
Δ = 1 − 4*0,5*0,25 = 1 − 0,5 =
	2

	1		√2
√Δ =		=
	√2		2

	√2   1 −   2
x =		= 1 − 0,5 √2 lub x = 1 + 0,5√2 > 1 − odpada
	1

P '(x) = 0 ⇔

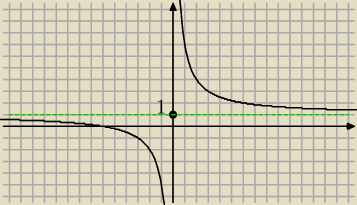
J: Zad 6) ZW = (−∞,1) U (1,+∞)

Janek191: Wtedy

	1 − 0,5√2 − 0,5
y =		= 1 − 0,5√2
	1 − 0,5√2 − 1

więc y = x oraz x + y = ( 1 − 0,5√2) + ( 1 − 0,5 p{2]) = 2 − √2 czyli z = 1 − ( x + y) = 1 − ( 2 − √2) = √2 − 1 Odp. x = y = 1 − 0,5√2 , z = √2 − 1 ============================= Jest to trójkąt prostokątny równoramienny.

J: Zad 5) coś Ty sie uparł na tą pochodną ? suma odwrotności pierwiastków nie przyjmuje najmniejszej wartości, natomiast przyjmuje największą równą 2 , dla k = 0

J: Zad 2) oczywiście

Janek191: z.5 czy z. 2 ?