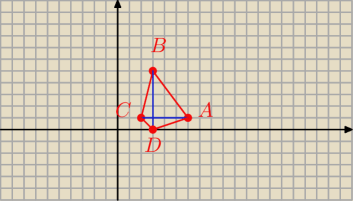
→
AC = [ 2 − 6, 1 − 1] = [ − 4, 0 ]
D = ( x , y)
x = 3
więc
D = ( 3 , y)
→
BD = [ 3 − 3, y − 5 ] = [ 0 , y − 5 ]
Iloczyn skalarny
→ →
AC o BD = − 4 *0 + 0*( y − 5) = 0 więc odcinki BD i AC są prostopadłe.
→
DC = [ 2 − 3 , 1 − y ] = [ − 1 , 1 − y ]
→
musi być równoległy do AB, więc
3*[ − 1 , 1 − y] = [ − 3 , 4]
[ − 3, 3 − 3 y ] = [ − 3 , 4]
3 − 3y = 4
3 y = − 1
| 1 | ||
y = − | ||
| 3 |
| 1 | ||
D = ( 3 , − | ] | |
| 3 |